0 导读

现实中会遇到多分类任务。虽然我们可以用神经网络直接建模多分类问题，但在机器学习的早期，一般模型只能解决二分类问题，因此有必要了解如何将二分类问题推广到多分类问题。

1 思路

考虑\(N\)个类别\(C_{1},C_{2},...C_{N}\)，多分类学习的基本思路是“拆解法”，即将多分类任务拆解为若干个二分类任务。具体地，先对原问题进行拆分，然后为拆分出的每个二分类任务训练一个分类器；在测试时，对这些分类器的预测结果进行集成以获得最终的多分类结果。由以上分析可知，关键是如何拆分以及如何集成。对于给定数据集:

一般的拆分策略有三种：

• 一对一（OvO）
• 一对其余（OvR）
• 多对多（MvM）

1.1 一对一

OvO将N个类别两两配对，从而产生\(N(N-1)/2\)个二分类任务，例如OvO将为区分类别\(C_{i}\)和\(C_{j}\)训练一个分类器，该分类器把\(D\)中的\(C_{i}\)类样例作为正例，\(C_{j}\)类样例作为反例。在测试阶段，新样本同时交给所有分类器，于是可得到\(N(N-1)/2\)个分类结果，把预测的最多的类别作为最终分类结果。

1.2 一对其余

OvR每次将一个类别的样例作为正例、所有其他类的样例作为反例，这样可以训练出\(N\)个分类器。在测试阶段若只有一个分类器预测为正例，则对应的类别标记作为最终分类结果。若有多个分类器预测为正例，则通常考虑各分类器预测的置信度，将置信度最大的类别标记作为最终分类结果。

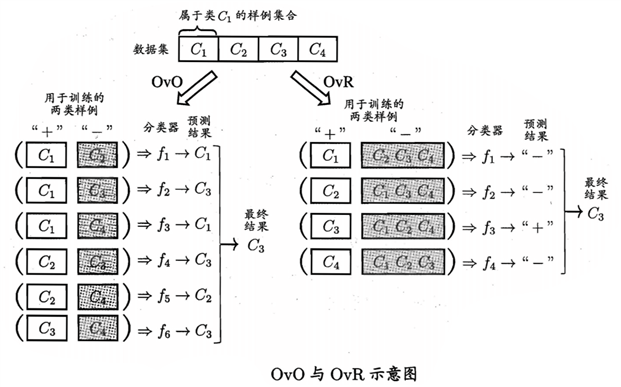
上图是OvO和OvR的示意图。易知，OvR需要训练N个分类器，OvO需要训练N(N-1)/2个分类器，素偶i，OvO的存储开销和测试开销比OvR更大。但在训练阶段，OvO的没个分类器只用到了一部分数据集，而OvR的每个分类器都用到了全部的数据集，因此，OvO的训练开销比OvR更小。在预测性能方面，两者通常是差不多的。

1.3 多对多

MvM每次将若干个类作为正类，若干个其他类作为反类。MvM的正反类构造通常用一种成为“纠错输出吗”（ECOC）的技术。ECOC是将编码的思想引入类别拆分中，并尽可能在解码过程中具有容错性。ECOC的工作过程主要分为两步：

• 编码：对N个类别做M此划分，每次划分将一部分类别划为正类，一部分划为反类，形成一个二分类训练集；这样一共产生M个训练集，可训练出M个分类器。
• 解码：M个分类器分别对测试样本进行预测，这些预测标记组成一个编码，将这个预测编码与每个类别各自编码进行比较，返回其中距离最小的类别最为最终类别。

2 类别不平衡问题

类别不平衡问题是指分类任务中不同类别的训练样本数量差别很大。即使原始数据集中各种类别的样本数量相差不大，但是进行OvO或OvR划分的时候也很容易出现类别不平衡的情况。类别不平衡会导致我们的分类结果失去意义，例如在含有100个样本的数据集中，有98个样本是反例，只有两个样本是正例，那么分类器只需要简单地将预测结果全部输出为反例即可取得98%的正确率，然而这样的分类器没有任何价值，即使其准确率较高，但是它无法识别正例，而实际问题往往更关注正例。
解决样本不平衡问题一般有如下三种方式（假设原始数据反例多，正例少）：

• 欠采样（也称下采样）
  去除一些反例使得正反例数目差不多。如果简单地丢弃一部分反例会损失很多信息，可能会导致欠拟合。一种有效的欠采样方法是EasyEnsemble，利用集成学习的机制，将反例划分为若干个集合供不同的学习器使用，这样每个学习器看起来都进行了欠采样，但是从全局看来却不会丢失重要信息。

• 过采样（也称上采样）
  增加一些整理使得正反例数目差不多。过采样不能对原始样本进行重复的采样，这样会导致严重的过拟合。一个代表性的过采样方法是通过对训练集里的正例进行插值来产生额外的正例。

• 再缩放
  以线性分类器\(y=wx+b\)为例，在对新样本进行分类时，会将预测值与一个指定的阈值进行比较，如\(y>0.5\)预测为正类，否则预测为反类。\(y\)表达了正例的可能性，几率\(\frac{y}{1-y}\)则表达了正例的可能行与反例的可能性之比，阈值设为0.5表明分类器认为真实类别是正、反例的可能性相同。$$若 \frac{y}{1-y} > 1 则预测为正$$然而当正反例数目相差较大时，令\(m^{+}\)表示正例数目，\(m^{-}\)表示反例数目，则观测几率是\(\frac{ m^{+} }{ m^{-} }\)

但是我们的分类器是基于公式\(\frac{y}{1-y} > 1\)进行决策的，因此需对预测值进行调整。
只需令：

3 参考

《机器学习》——周志华

原文：https://www.cnblogs.com/foghorn/p/15185340.html