1.风险函数定义

风险函数（risk function）=期望损失（expected loss），可以认为是平均意义下的损失。

例如：下面的对数损失函数中，损失函数的期望，就是理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失。

风险函数有两种，不考虑正则项的是经验风险（Empirical Risk），考虑过拟合问题，加上正则项的是结构风险（Structural Risk）。

监督学习的两个基本策略：经验风险最小化（ERM）和结构风险最小化（SRM）。

（1）经验风险（Empirical Risk）

经验风险=经验损失=代价函数

给定一个数据集，模型f(x)关于训练集的平均损失被称为经验风险(empirical risk)或经验损失(empirical loss)。

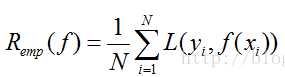
这个公式的用意很明显，就是模型关于训练集的平均损失（每个样本的损失加起来，然后平均一下）。在实际中用的时候，我们也就很自然的这么用了。

经验风险最小化（ERM），就是认为经验风险最小的模型是最优的模型，用公式表示：

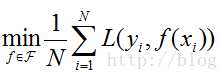
这个理论很符合人的直观理解。因为在训练集上面的经验风险最小，也就是平均损失越小，意味着模型得到结果和“真实值”尽可能接近，表明模型越好。

（2）结构风险（Structural Risk）

结构风险，就是在经验风险上加上一个正则化项（regularizer）或者叫做罚项（penalty term），即

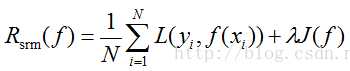
当样本容量不大的时候，经验风险最小化模型容易产生“过拟合”的问题。为了“减缓”过拟合问题，就提出了结构风险最小的理论。

结构风险最小化（SRM），就是认为，结构风险最小的模型是最优模型，公式表示：

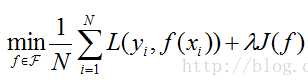
参考：https://blog.csdn.net/xierhacker/article/details/53366723?utm_source=copy

2.风险函数与对数损失函数

原文：https://www.cnblogs.com/sybil-hxl/p/13653932.html