卷积神经网络
卷积神经网络
什么是卷积
图像的表示
例如mnist灰度图像,0~ 255表示该位置图像的值,在一般数据处理的时候我们将数据除以255,让灰度值在0~1的范围之内。
一般的图片是彩色的,也就是拥有RGB通道,使用三张表来存储这张图片的三个通道的每个数值每个数值也是0~255
卷积
通过在图像上生成一个小窗口(感受野),来在图片上进行移动,并共享参数(局部相关性)
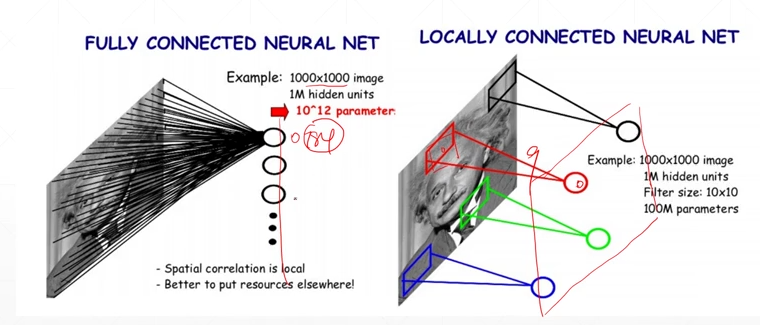
从全连接的784条线变为只进行对应点周边的线(9条)
不同的kernal就代表的是不同的模式,有可能是blur,有可能是edge detect,从而产生的map也是不一样的
例子:
layer = torch.nn.Conv2d(1,3,kernel_size=3,stride=1,padding=0)
这里的第一个参数表示input channel(黑白就是1,彩色就是3)
第二个参数表示kernel的数量为3
第三个参数表示kernel的大小
第四个参数表示kernel移动的步长
第五个参数表示最外围是不是要进行补充padding
核函数
一个在彩色图像中使用的核函数的shape:【3,3,3】
第一个3表示是在图像的RGB三个通道进行计算(这个要与输入图像的相应通道数相等);在核函数计算的时候,每个通道的核函数计算完毕输出的3个数字最后相加。
第二与第三个3表示核函数的大小是3*3的
多个核函数的shape:【16,3,3,3】
表示其中存在16个kernel核函数,一般说kernel的channel就说的是这个16
例子:
输入 :【batch_size,3,28,28】
一个kernel:【3,3,3】
多个kernel:【16,3,3,3】
输出:【batch_size,16,28,28】(padding为1)
池化
下采样(downsample):
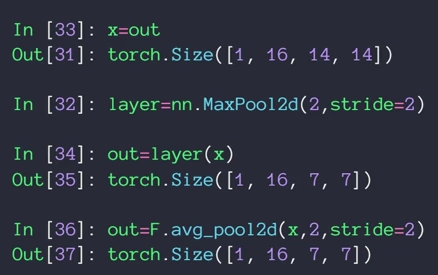
最大池化(maxpooling)——一般stride=2
平均池化(avg pooling)——一般stride=2
上采样(upsample):
复制
例子:
batch norm
image normalization
在不可避免需要使用sigmoid激活函数的时候,如果数据的输入太小或者太大的话,会导致梯度消失,梯度的更新几乎停止,这样对训练时间的消耗以及相应的效果都会有影响,所以我们要在输入数据的时候进行数据的处理,将数据的输入控制在0~1之间,最好的情况就是数据的均值在0附近
使用normalization,收敛的速度会变快,而且精度也会提升,模型变得更稳定,使得对于超参数的调整不再那么敏感
例子:
normalize = transfroms.Normalize(mean=[0.485,0.456,0.406],std=[0.229,0.224,0.225])
mean表示图像的RGB三个通道的均值,而std则是相应的方差,具体的计算方法就是:
(\(Xr\)-0.485)/0.229 (\(Xg\)-0.456)/0.224 (\(Xb\)-0.406)/0.225
batch normalization
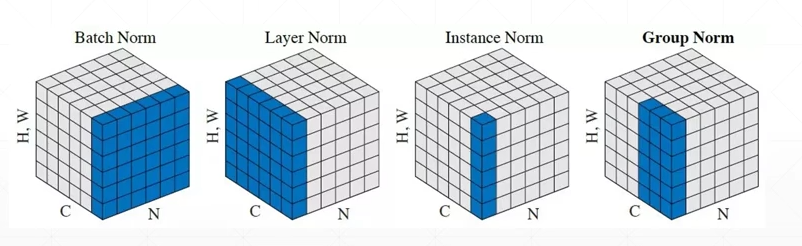
如图,其中c表示一个batch的数据的channel数,N表示数据的数量,H、W表示图片的长与宽。
所以一个batch的数据为【N,C,H,W】——【N,C,HW】
其中batch norm表示以每个channel为切入对象,会生成一个【C】的数据,分别表示C个各自channel下N张图片的一个均值
同理layer morm表示N张各自图片下C个channel的一个均值
batch normalization详细内容
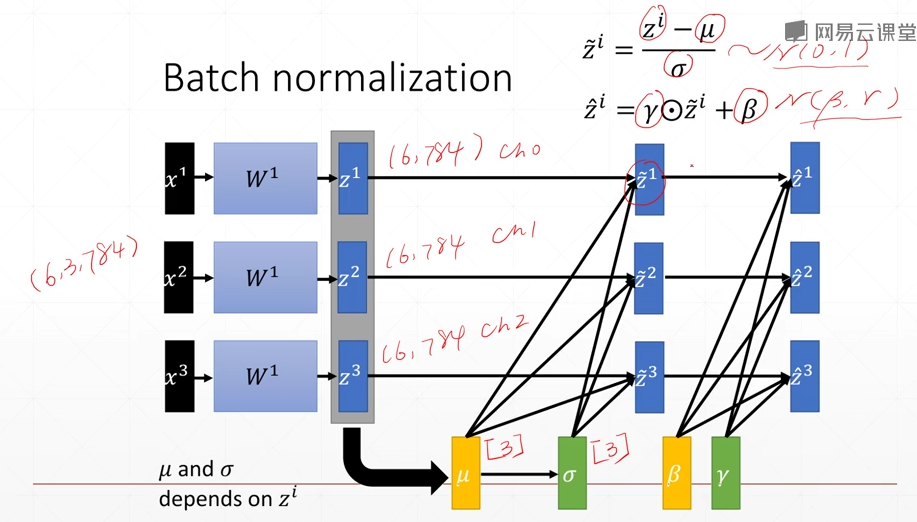
如图,有三个channel,我们收集三个channel的信息,可以得到μ以及δ,然后将原来的数据减去μ后整体除以δ,就可以将数据转换为一个接近以0为均值,以1为方差的一个分布(N(0,1))
然后乘以一个γ后加一个β,将数据变为(N(β,γ))
μ、δ是通过当前batch的数据进行统计出来的,running-μ、running-\(δ^2\)表示总的均值与方差;而γ、β则需要参考梯度的信息
例子:
x = torch.rand(100,16,784)
layer = nn.BatchNorm1d(16)#这里的16必须与上面的16一致
out = layer(x)#进行一次forward
print(layer.running_mean)#总均值
tensor([0.0499, 0.0500, 0.0500, 0.0498, 0.0501, 0.0502, 0.0498, 0.0500, 0.0502,
0.0501, 0.0500, 0.0499, 0.0502, 0.0502, 0.0500, 0.0500])
print(layer.running_var)#总方差
tensor([0.9083, 0.9083, 0.9084, 0.9084, 0.9083, 0.9083, 0.9084, 0.9083, 0.9083,
0.9083, 0.9083, 0.9083, 0.9084, 0.9084, 0.9084, 0.9083])
通过结果我们可以看到初始的数据是rand()即均匀分布(0,1),那么均值就是0.5,而layer.running_mean都是在0.5附近,而方差在1附近,而layer.running_var也接近1
由于初始的数据是【100,16,784】,HW在一起,所以使用的是nn.BatchNorm1d()函数,如果数据是【100,16,28,28】就是nn.BatchNorm2d()函数
类中的参数说明:
training:表示此时是在train的模式还是test的模式
在test的时候μ、δ无法统计,直接使用running-μ、running-\(δ^2\)赋值,而test不需要后向传播,γ、β不需更新,所以要在代码中调用
layer.eval()
进行模式的变换
affine:表示是否需要进行γ、β的学习更新,日过设置为false的话那么这个γ就自动为1,β自动为0,且不自动更新
深度残差网络
思路
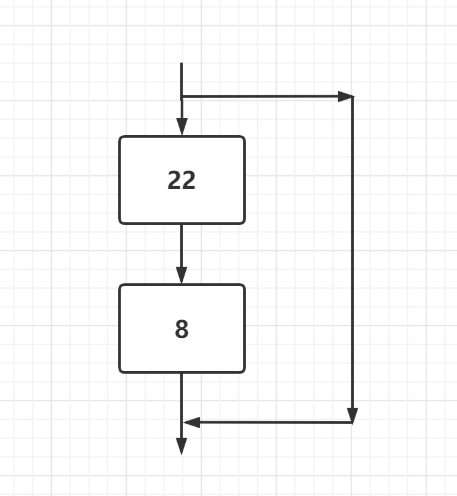
随着网络的加深,累计的参数变多,越容易导致梯度下降或者梯度爆炸,于是现象就是更深的网络有着更强大的表达,但是随着网络的增加,最终的效果却不好,于是resnet的思路就是在进行网络加深的时候进行一个类似短路的操作,保证最终的效果
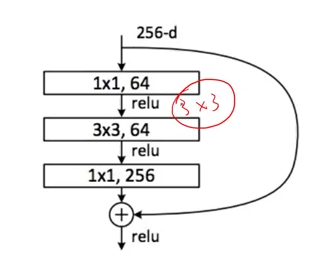
通过这样的结构,中间网络的参数减小,导致更深层的网络的实现成为可能。
例子:
class ResBlk(nn.Module):
"""
resnet block
"""
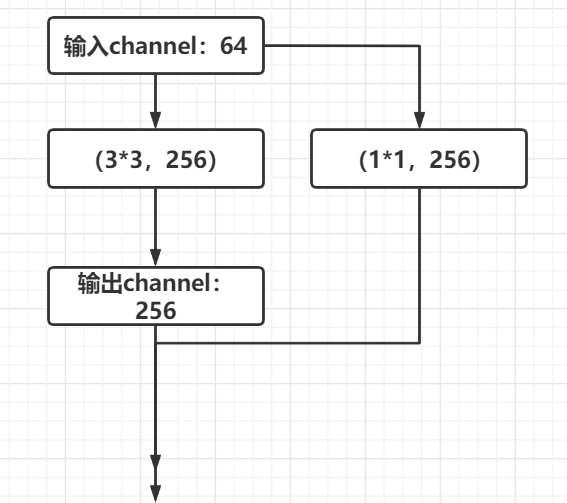
def __init__(self, ch_in, ch_out):# ch_in, ch_out不一定一致,假设ch_in为64,ch_out为256
"""
:param ch_in:
:param ch_out:
"""
super(ResBlk, self).__init__()
self.conv1 = nn.Conv2d(ch_in, ch_out, kernel_size=3, stride=1, padding=1)
self.bn1 = nn.BatchNorm2d(ch_out)
self.conv2 = nn.Conv2d(ch_out, ch_out, kernel_size=3, stride=1, padding=1)
self.bn2 = nn.BatchNorm2d(ch_out)
self.extra = nn.Sequential()
if ch_out != ch_in:#如果输入的channel与输出的channel不相同,将输入channel变为输出channel
# [b, ch_in, h, w] => [b, ch_out, h, w]
self.extra = nn.Sequential(
nn.Conv2d(ch_in, ch_out, kernel_size=1, stride=1),
nn.BatchNorm2d(ch_out)
)
def forward(self, x):
"""
:param x: [b, ch, h, w]
:return:
"""
out = F.relu(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
# short cut.
# extra module: [b, ch_in, h, w] => [b, ch_out, h, w]
# element-wise add:
out = self.extra(x) + out
return out
原文:https://www.cnblogs.com/Jason66661010/p/13618739.html
