12-并查集 UnionFind
时间:2020-07-03 20:20:43
收藏:0
阅读:56
目录
1、简介
? 并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题
- union(p,q),合并两个元素所在的集合
- isConnected(p,q),查询两个元素是否属于一个集合
2、实现
2.1、实现思路
- 将每一个元素看作是一个结点
- 独立的结点指向自己本身
- 合并两个结点所属集合,只需要让两个结点的根结点连接即可
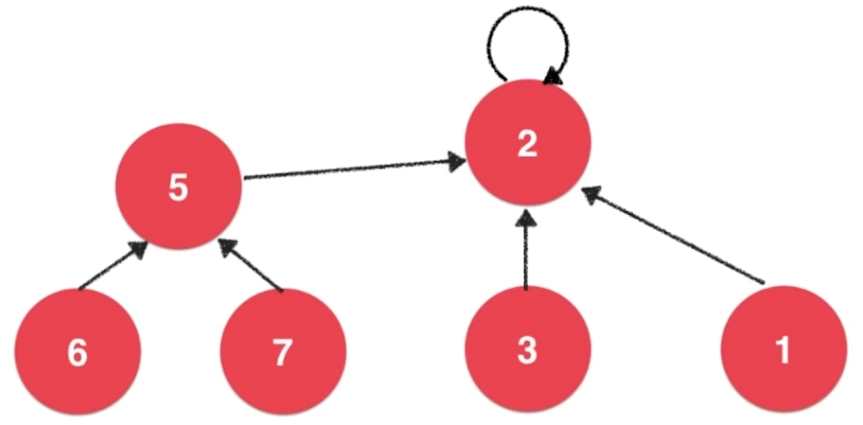
- 判断两个结点是否属于一个集合,只需要查看它们的根结点是否为同一个结点即可
2.2、接口
public interface unionFind {
//p,q不是具体的元素,而是像元素在数组的索引
int getSize();
// 查看元素p和元素q是否属于一个集合
boolean isConnected(int p, int q);
// 合并元素p和元素q所属的集合
void unionElement(int p, int q);
}
2.3、初始状态
每一个结点指向自己,这种状态可以使用数组进行表示:每一个结点对应数组中的相应索引处的值。
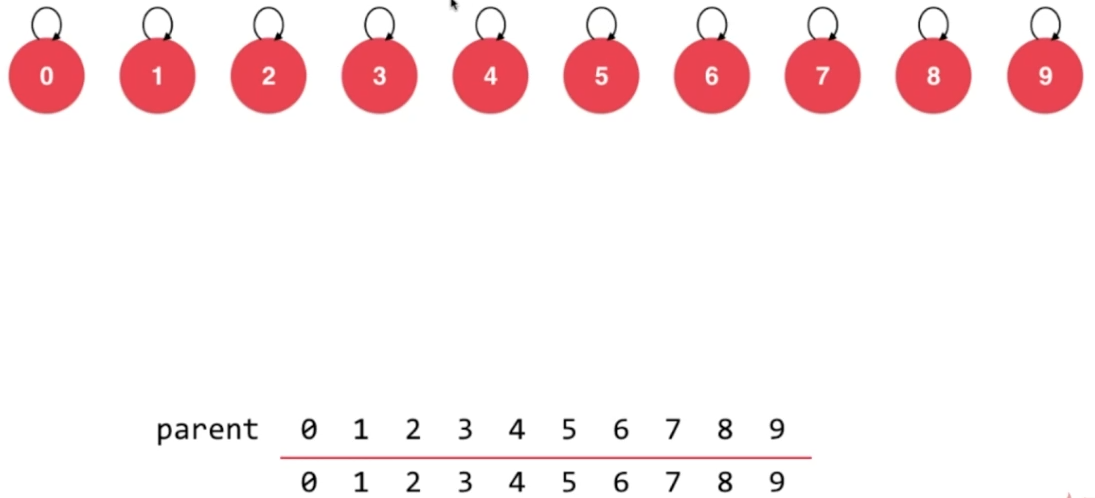
2.4、union操作
- union 4,3
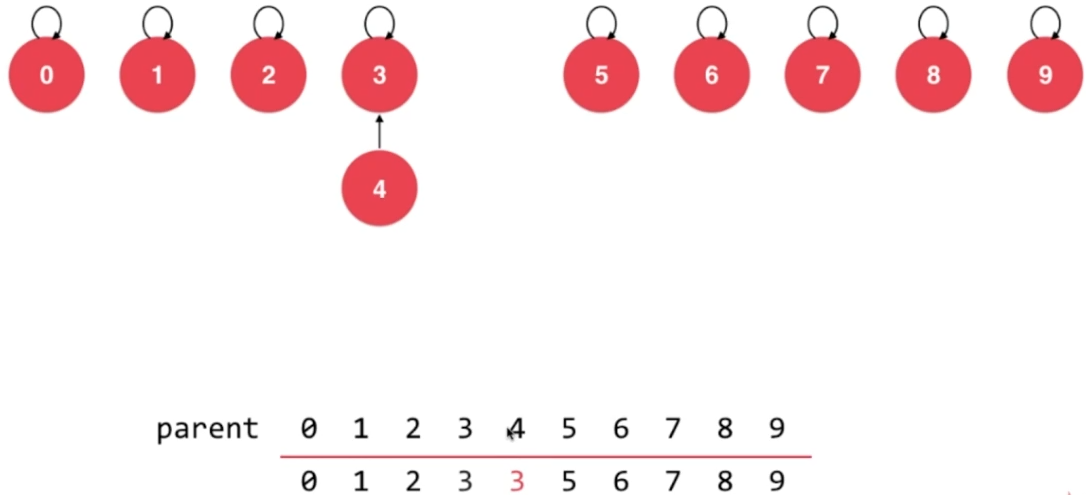
- union 3,8
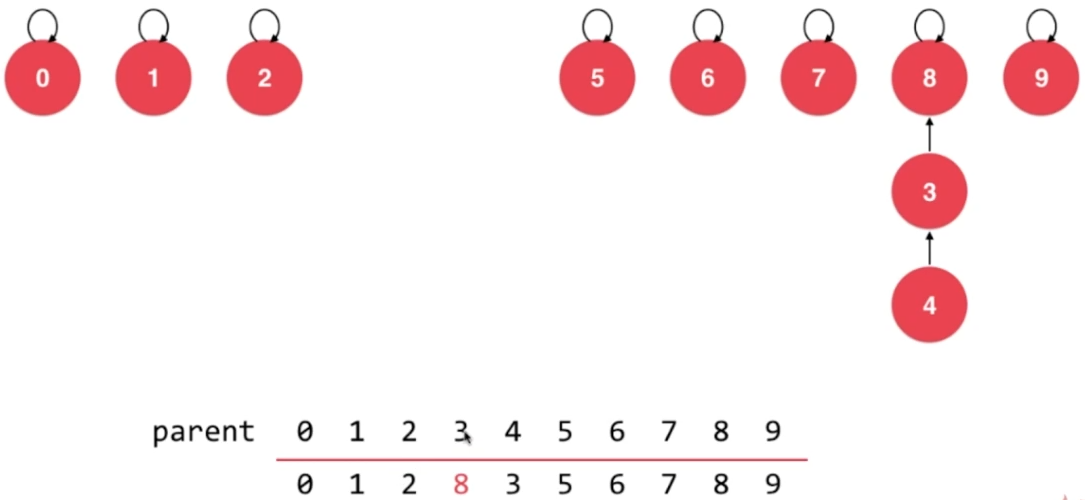
- union 9,4
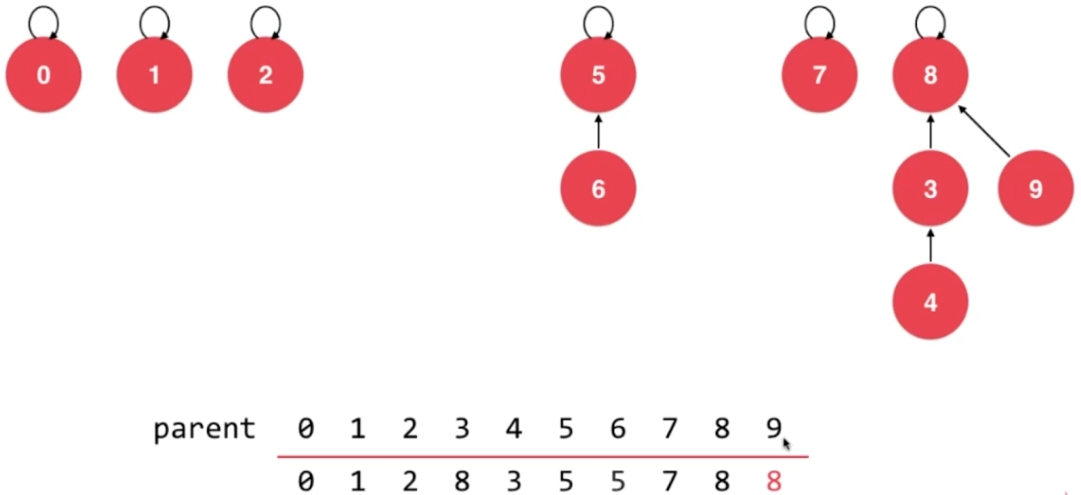
- union 2,1
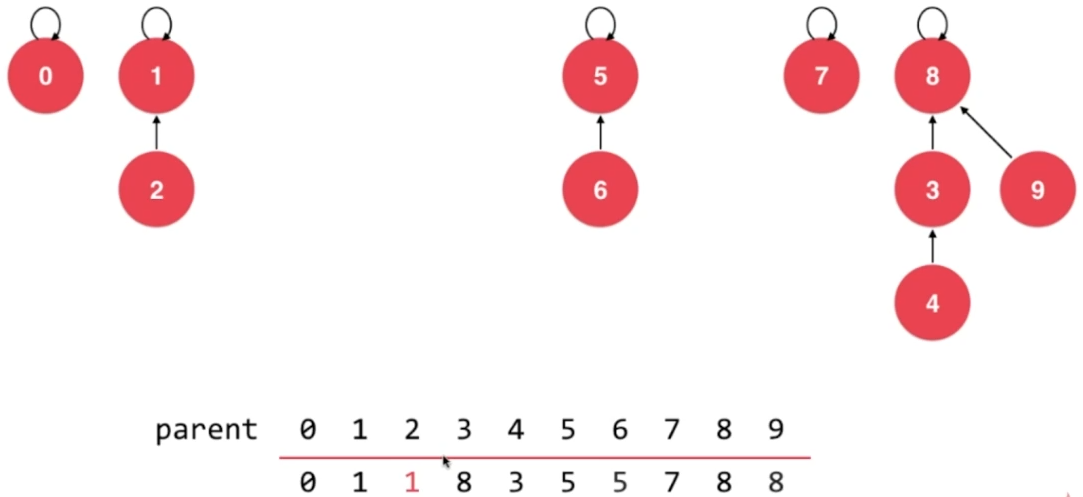
- union 5,0
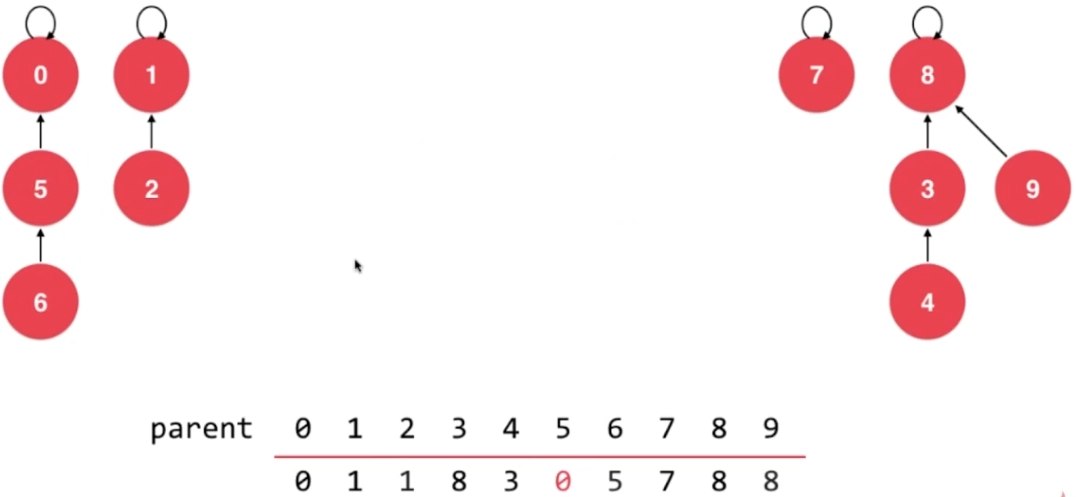
- union 7,2
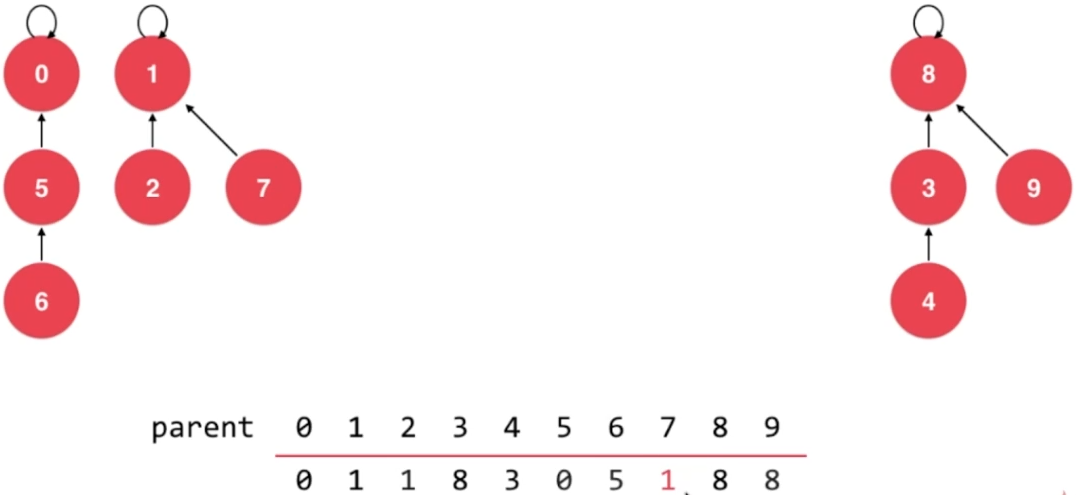
- union 6,2
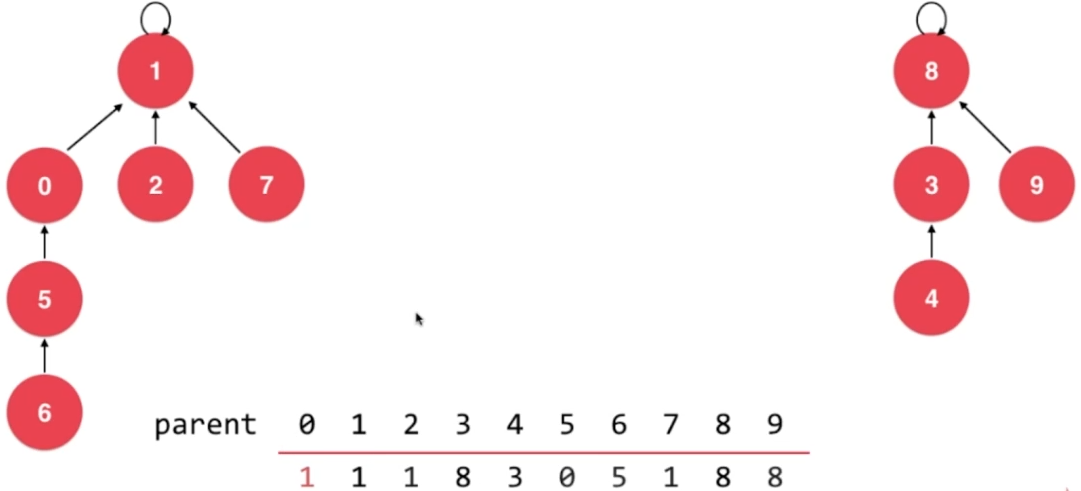
2.5、代码
public class UnionFind_2 implements unionFind {
private int[] parent;
// 每一个元素单独属于一个集合
public UnionFind_2(int size) {
parent = new int[size];
for(int i = 0; i < size; i++){
parent[i] = i;
}
}
@Override
public int getSize() {
return parent.length;
}
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
@Override
public void unionElement(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
parent[pRoot] = qRoot;
}
// 查找元素p对应的集合编号
private int find(int p){
while (p != parent[p])
p = parent[p];
return p;
}
}
3、代码优化
3.1、基于size的优化
union 8,9
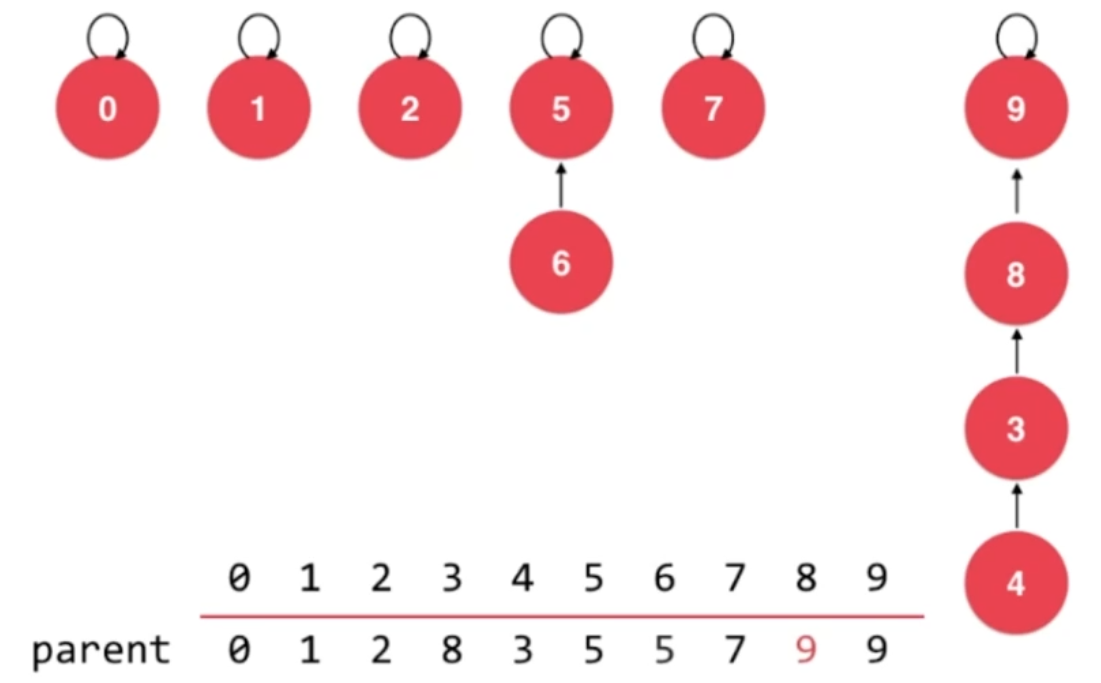
显然,这样的合并操作有可能会不断增加树的高度,进而导致isConnected操作的复杂度过大。
解决方法:让结点数少的树的根结点指向结点数多的树的根结点。
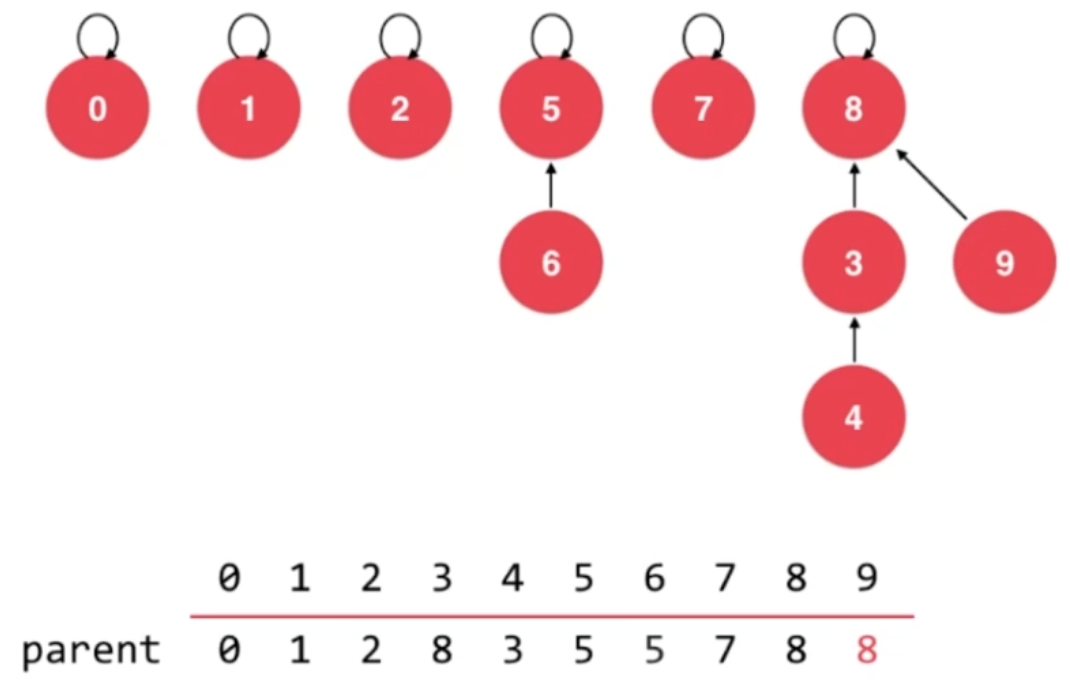
public class UnionFind_3 implements unionFind {
private int[] parent;
private int[] size; //size[i] 表示以i为根的集合中元素的个数
public UnionFind_3(int size) {
parent = new int[size];
this.size = new int[size];
for(int i = 0; i < size; i++){
parent[i] = i;
this.size[i] = 1;
}
}
@Override
public int getSize() {
return parent.length;
}
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
@Override
public void unionElement(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
if(size[pRoot] < size[qRoot]){
parent[pRoot] = qRoot;
size[qRoot] += size[qRoot];
}
else{
parent[qRoot] = pRoot;
size[pRoot] += size[qRoot];
}
}
private int find(int p){
while (p != parent[p])
p = parent[p];
return p;
}
}
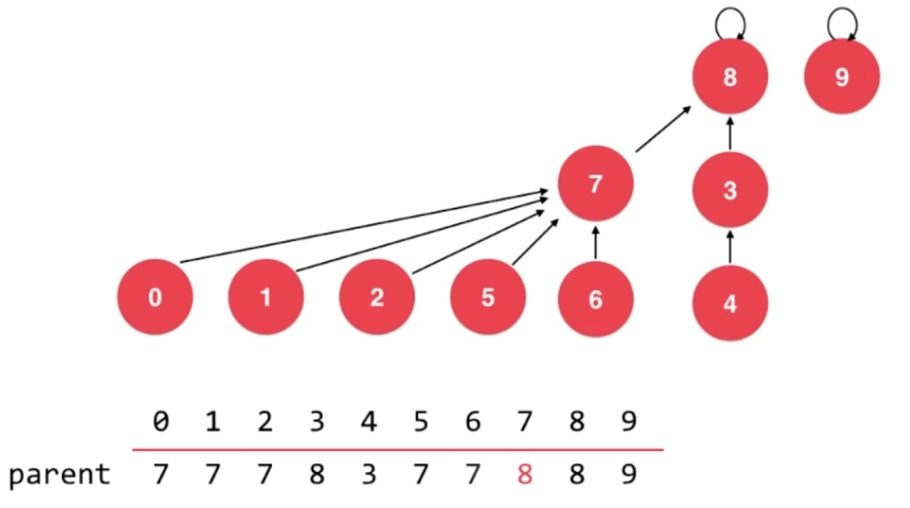
3.2、基于rank的优化
union 7,8
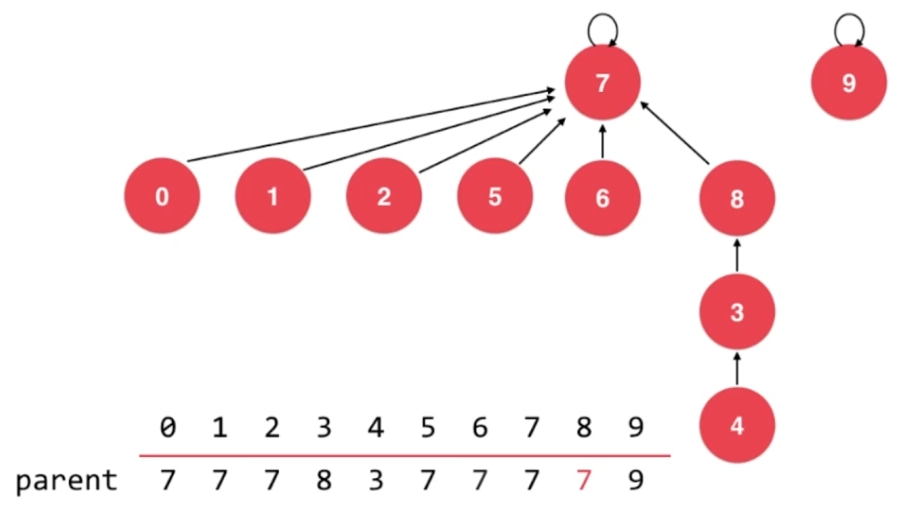
很明显,按照之前的优化方式,树的高度将增大。
解决方法:让高度小的树的根结点指向高度大的的树的根结点。
与前面基于size的优化相比,基于rank的优化可以减少树的高度增长的概率。
public class UnionFind_4 implements unionFind {
private int[] parent;
private int[] rank; // rank[i] 表示以i为根的集合所表示的树的高度
public UnionFind_4(int size) {
parent = new int[size];
this.rank = new int[size];
for(int i = 0; i < size; i++){
parent[i] = i;
rank[i] = 1;
}
}
@Override
public int getSize() {
return parent.length;
}
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
@Override
public void unionElement(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
if(rank[pRoot] < rank[qRoot]){
parent[pRoot] = qRoot;
}
else if(rank[pRoot] > rank[qRoot]){
parent[qRoot] = pRoot;
}else {
parent[qRoot] = pRoot;
rank[pRoot] += 1;
}
}
private int find(int p){
while (p != parent[p])
p = parent[p];
return p;
}
}
4、路径压缩
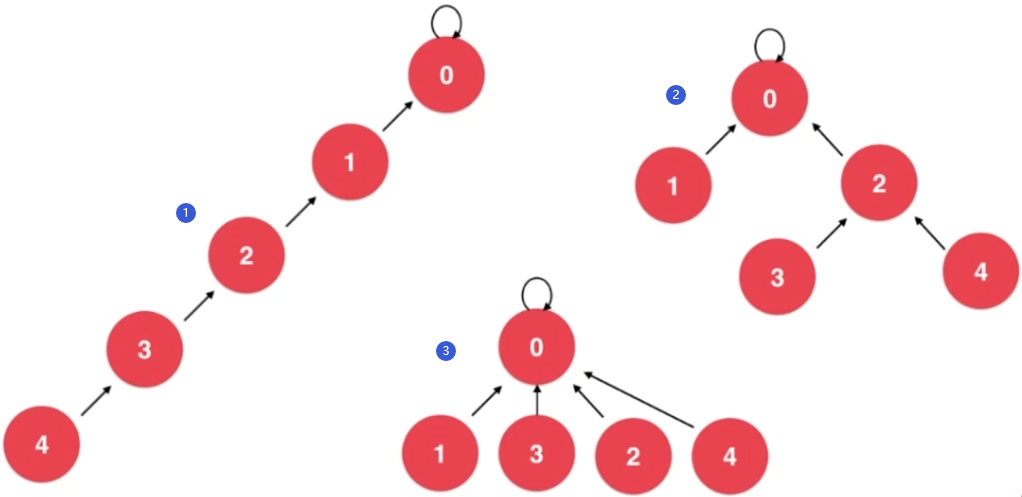
理想情况下,一棵树的形状应该是③ :树的高度尽可能的小。
为此我们需要进行路径压缩,减小树的高度,此过程设计在find方法中,因为在合并两个结点前要进行find操作。
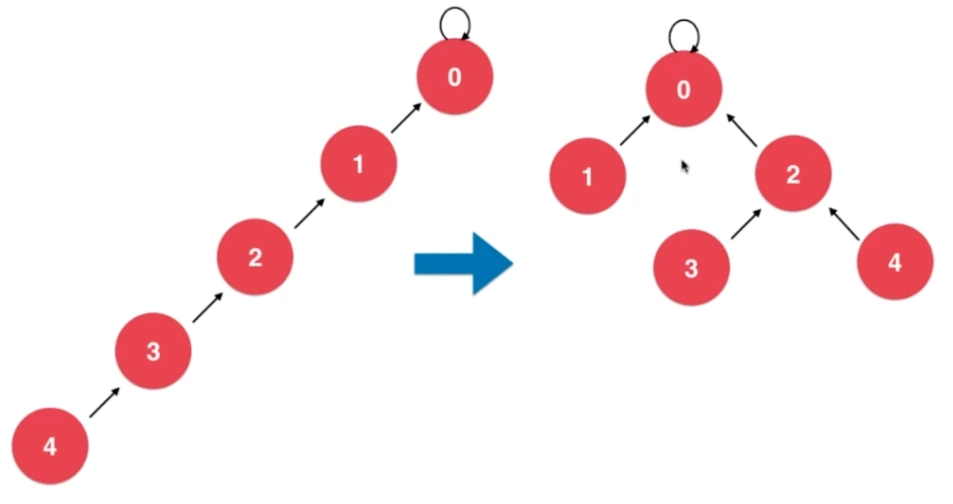
4.1、压缩方式一
private int find(int p){
while (p != parent[p]){
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
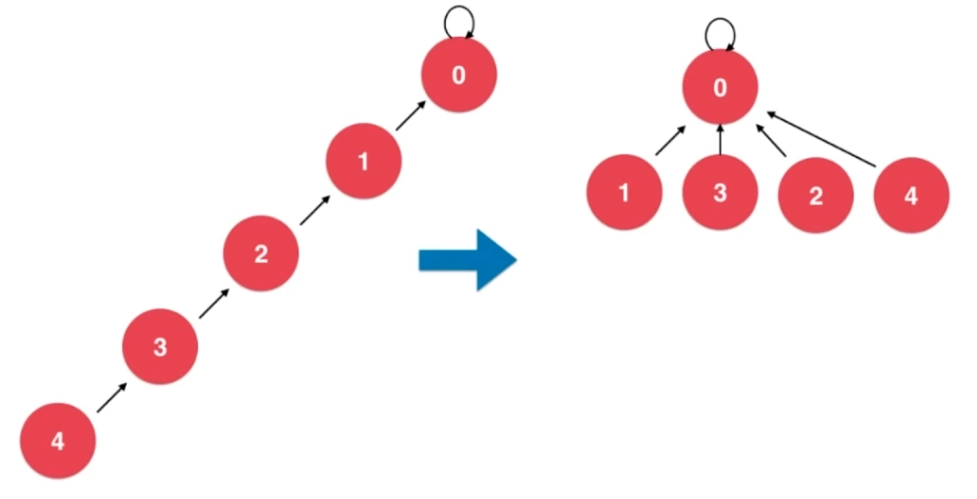
4.2、压缩方式二
// 递归实现路径压缩
private int find(int p){
if(p != parent[p]){
parent[p] = find(parent[p]);
}
return parent[p];
}
5、测试
private static long getRunTimeNano(UnionFind unionFind, int times){
int size = unionFind.getSize();
Random random = new Random();
long startTime = System.nanoTime();
for(int i=0; i<times; i++){
int a = random.nextInt(size);
int b = random.nextInt(size);
unionFind.unionElement(a, b);
}
for(int i=0; i<times; i++){
int a = random.nextInt(size);
int b = random.nextInt(size);
unionFind.isConnected(a, b);
}
long endTime = System.nanoTime();
return endTime - startTime;
}
public static void main(String[] args) {
int size = 100000;
int times = 100000;
UnionFind_6 unionFind_6 = new UnionFind_6(size);
long runTime = getRunTimeMills(unionFind_6, times);
System.out.println(runTime);
}
原文:https://www.cnblogs.com/sout-ch233/p/13232298.html
评论(0)
