四个基本子空间
时间:2020-05-14 12:52:39
收藏:0
阅读:50
列空间的basis是消元时的主列(pivot)
行空间的basis就是消元得到行最简形对应的非零行;
零空间的basis是自由列F
左零空间basis是对应矩阵左乘E行变换时得到行最简形对应的零行时E对应行。
空间的维数就是由这些主列/或者是自由列/行的数目确定的
而主列的个数就是矩阵的秩
什么是Rm,Rn,看一个向量由几个分量构成的就可以了
比如列向量由m个分量构成,那么就是Rm空间里的subspace;
向量可以看做空间中的一点。
1.行空间的正交补是零空间
列空间的正交补是左零空间
2.行空间的维数加零空间的维数是n
列空间的维数加左零空间的维数是m
3.行空间与零空间的直和是Rn
列空间与左零空间的直和是Rm
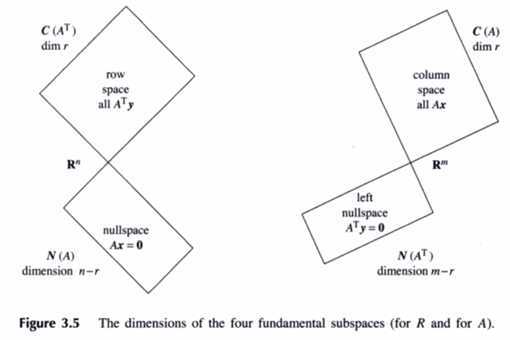
正交子空间不唯一 两个子空间的关系是正交
正交补空间唯一 子空间是另一子空间的正交补
原文:https://www.cnblogs.com/wwqdata/p/12887625.html
评论(0)
