数据结构之查找算法

时间：2020-04-25 12:11:41 收藏：0 阅读：43

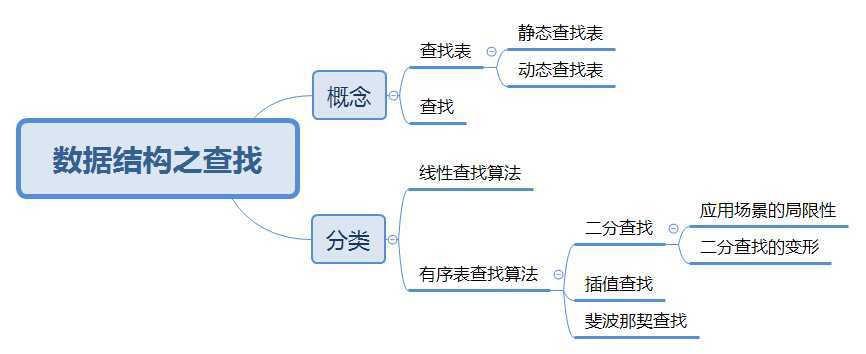
技术分享图片

一、基本概念

查找表：由相同类型的元素构成的集合
静态查找表：进行查找时，没有频繁的删除和插入操作
动态查找表：查找时，不仅存在查找操作，还有元素的插入与删除操作
查找：给定一个确定的值，在查找表中寻找与给定值相同的数据元素

二、分类

线性查找算法
核心思想：从头（尾）依次与查找表中的元素进行比较
注意：查找表可以是有序表也可以是无序表
复杂度分析
最好时间复杂度：O（1）
最坏时间复杂度：O（n）
平均时间复杂度：O（n）
优缺点：不适合数据量大的查找；适合数据量小的查找

代码实现

/查找唯一的一个值
public static int searchXian(int[] arr,int value){
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == value){
            return i;
        }
    }
    return -1;
}
//优化，利用哨兵思想，上述每次都要判断i是否越界，这步操作可以省去

//查找多个相同的值
public static ArrayList<Integer> searchXian11(int[] arr,int value){
    ArrayList<Integer> arrayList = new ArrayList<>();
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == value){
            arrayList.add(i);
        }
    }
    return arrayList;
}

有序表查找
二分查找算法
核心思想：类似于分治思想。每次通过跟区间的中间元素进行比较，将待查找的区间缩小为之前的一半，直到找到要查找的元素
注意：针对的是有序表；若是无序表，需要进行排序，然后利用二分查找。
复杂度分析
最好时间复杂度：O（1）
最坏时间复杂度：O（n）
平均时间复杂度：O（log n）
场景局限性：

二分查找依赖的是顺序表，即数组。链表这种链式表不适合，因数组支持下标随机访问，时间复杂度为O（1），而链表为O（n）
二分查找针对的是有序表，同时不存在频繁的数据插入与删除的静态数据。此时只需要一次排序，多次二分查找，排序的成本可被均摊，二分查找的边际成本会比较低
数据量太小不适合二分查找。数据量小的情况下，二分查找与顺序查找没有太大的区别。特例：数组中存储的都是长度超过300的字符串，此时进行比较操作会比较耗时，推荐使用二分查找
数据量太大也不适合二分查找。这个主要从内存的连续来分析，因为二分查找的底层是数组，而数组对内存空间的要求是连续的存储空间，所以即使剩余的存储空间很大，但是不连续，也无法利用二分查找。
但凡能用二分查找的，基本上都倾向于用散列表或者二叉查找树。二分查找更适合“近似”查找问题

二分查找的变形体（默认元素从小到大）,针对的是有序数组中存在重复的元素
查找第一个值等于给定值的元素
查找最后一个值等于给定值的元素
查找第一个大于等于给定值的元素
查找最后一个小于等于给定值的元素
代码实现

 1 //利用递归的方法，数组中不存在重复的元素
 2 public static int binarySearch(int[] arr, int low, int high, int value){
 3 //首先low > high ,说明没有找到
 4 if(low > high){
 5 return -1;
 6 }
 7 int mid = (low + high)/2;
 8 if(arr[mid] == value){
 9    return mid;
10 }else if(arr[mid] > value){
11    return binarySearch(arr, low, mid - 1, value);
12 }else{
13    return binarySearch(arr, mid + 1, high, value);
14 }
15 }

//此时为有序数组，且存在重复的数值，并返回所有的下标。找到mid时，此时不返回，沿mid向两边扫描，将所有的下标值添加到ArrayList集合中
public static ArrayList<Integer> binarySearch1(int[] arr,int low,int high,int findVal){
    //定义一个数组集合，用于存放下标
    ArrayList<Integer> arrayList = new ArrayList<>();
    //当low>high时，说明递归完没有找到值
    if (low > high){
        return new ArrayList<>();
    }
    int mid = (low + high)/2;
    if (findVal > arr[mid]){
        return binarySearch1(arr,mid + 1,high,findVal);//向右递归
    }else if(findVal < arr[mid]){
        return binarySearch1(arr,low,mid - 1,findVal);//向左递归
    }else{
        int tempLeft = mid - 1;
        int tempRight = mid + 1;
        while(arr[tempLeft] == arr[mid] && tempLeft >= 0){
            arrayList.add(tempLeft);
            tempLeft -= 1;
        }
        arrayList.add(mid);
        while (arr[tempRight] == arr[mid] && tempRight <= arr.length - 1){
            arrayList.add(tempRight);
            tempRight += 1;
        }
        return arrayList;
    }
}

//非递归方法，数组中不存在重复的元素
public static int binarySearch1(int[] arr,int value){
    int low = 0;
    int high = arr.length - 1;
    while (low <= high){

　　　　　int mid = (low + high)/2;

        if (arr[mid] == value){
            return mid;
        }else if(arr[mid] > value){
            high = mid - 1;
        }else{
            low = mid + 1;
        }
    }
    return -1;
}
//编写二分查找代码的注意事项：
1.注意结束条件。low <= high
2.注意mid 的取值。（high + low）/2,当high和low 很大时，两者之和容易溢出。可以写成：low + (high - low)/2,若优化到极致的话，可以写为：low + ((high - low)>>1).原因：相比除法运算，计算机的位处理要快很多
3.high和low值的更新
4.O（1）常量级复杂度可能比O（log n）更高。例如：O（300000）和O（log n）相比，后者的执行效率会更高。

//查找第一个值等于给定值的元素
public static int binarySearch3(int[] arr, int value){
int low = 0;
int high = arr.length - 1;
if(low > high){
　　return -1;
}
while(low <= high){

int mid = low + ((high - low)>>1);

　　if(arr[mid] = value){
　　　　if(（arr[mid - 1] != value） || （mid == 0）){
　　　　　　return mid;
　　　　}else{
　　　　　　high = mid - 1;
　　　　}
　　}elseif(arr[mid] > value){
　　　　　　high = mid - 1;
　　}else{
　　　low = mid + 1;
　　}
}
}

//查找最后一个值等于给定值的元素
public static int binarySearch3(int[] arr, int value){
int low = 0;
int high = arr.length - 1;
if(low > high){
　　return -1;
}
while(low <= high){

int mid = low + ((high - low) >> 1);

　　if(arr[mid] = value){
　　　　if(（arr[mid + 1] != value） || （mid == arr.length - 1）){
　　　　　　return mid;
　　　　}else{
　　　　　　low = mid + 1;
　　　　}
　　}elseif(arr[mid] > value){
　　　　　　high = mid - 1;
　　}else{
　　　low = mid + 1;
　　}
}
}
//查找第一个大于等于给定值的元素
public static int binarySearch3(int[] arr, int value){

int low = 0;
int high = arr.length - 1;

if(low > high){
　　return -1;
}
while(low <= high){

int mid = low + ((high - low)>>1);

　　if(arr[mid] >= value){

　　　　if((arr[mid - 1] != value) || (mid == 0)){
　　　　　　return mid;
　　　　}else{
　　　　　　high = mid - 1;
　　　　}
　　}else{
　　　low = mid + 1;
　　}
}
}

//查找最后一个小于等于给定值的元素
public static int binarySearch3(int[] arr, int value){

int low = 0;
int high = arr.length - 1;

if(low > high){
　　return -1;
}
while(low <= high){

int mid = low + ((high - low)>>1);

　　if(arr[mid] <= value){

　　　　if((arr[mid + 1] != value) || (mid == arr.length - 1)){
　　　　　　return mid;
　　　　}else{
　　　　　　low = mid + 1;
　　　　}
　　}else{
　　　high = mid - 1;
　　}
}
}

插值查找算法
缘由：二分查找是以有序数组的区间的中间作为划分标准。那是否可以不以中间作为划分标准，而按照1/4或者1/8来划分呢？
定义：将给定的值与查找表中的最大最小关键字比较后再进行查找。
核心思想：mid = low + (value - arr[low])/(arr[high]-arr[low])
时间复杂度：O(log n)
适用场景：查找表比较长，数据分布比较均匀，插值比二分会好很多；但是如果存在极端的查找表，不建议使用插值查找。（来源于大话数据结构）
斐波那契查找算法

按照黄金分割的标准来划分有序数组
时间复杂度：O(log n)
优点：相比于二分查找，它只涉及加减操作，没有乘除操作

原文：https://www.cnblogs.com/zyj-0917/p/12770884.html