4.13 省选模拟赛 传销组织 bitset 强连通分量 分块

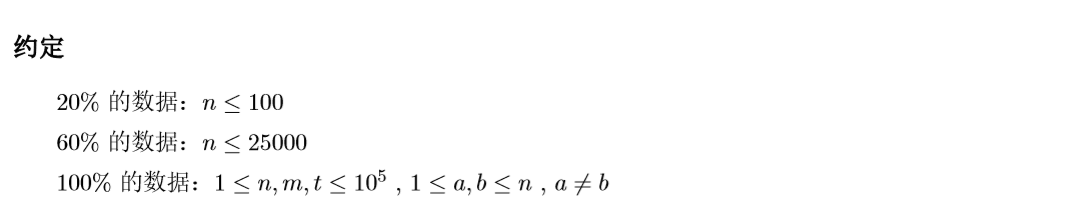
考试的时候昏了头 没算空间 这道题我爆零了。值得注意的是 一般认为bitset的空间是 int 的1/w倍

对于那m条边 无论如何构造 这m条关系都是存在的 题目其实是想让我们用这m条关系来计算给出的 t条关系是否合法。

合法把这m条边输出即可。

这道题 虽然不是多组数据 但是评测时开了subtask. 果然 判定对错的题目 基本上不给水分的机会...

缩过点之后 剩下的是可达性问题 这是一个经典问题 如果点不是类似于区间性的问题 最快也只能使用bitset来解决 这个大概是常识吧.

发现 mn/w 勉强可以卡过 但是会爆空间。

这种问题 算是很常见的问题 如 求5,6维偏序的时候 bitset空间容易爆 一般采用根号分治法。

对n个点进行分块 每次统计一个 块内的点对应的询问即可。

设 块大小为 S 那么数量为 n/S 每次统计一下 n/SmS/w=nm/w.

空间复杂度 nS/w.

可以发现 时间不会变得更差 空间变小 取S等于sqrt(n)即可。

//#include<bits\stdc++.h>
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<string>
#include<ctime>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<queue>
#include<deque>
#include<stack>
#include<vector>
#include<algorithm>
#include<utility>
#include<bitset>
#include<set>
#include<map>
#define ll long long
#define db double
#define INF 1000000000
#define ldb long double
#define pb push_back
#define get(x) x=read()
#define gt(x) scanf("%d",&x)
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define gc(a) scanf("%s",a+1)
#define rep(p,n,i) for(RE int i=p;i<=n;++i)
#define go(x) for(int i=lin[x],tn=ver[i];i;tn=ver[i=nex[i]])
#define fep(n,p,i) for(RE int i=n;i>=p;--i)
#define pii pair<int,int> 
#define mk make_pair
#define RE register
#define P 1000000007
#define S second
#define gf(x) scanf("%lf",&x)
#define pf(x) ((x)*(x))
#define ull unsigned long long
#define mod 998244353
using namespace std;
char buf[1<<15],*fs,*ft;
inline char getc()
{
    return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
    register int x=0,f=1;register char ch=getc();
    while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getc();}
    while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getc();}
    return x*f;
}
const int MAXN=100005;
int n,m,Q,len,top,id,cnt;
int s[MAXN],c[MAXN],low[MAXN],dfn[MAXN];
int lin[MAXN],ver[MAXN],nex[MAXN],ru[MAXN];
int lin1[MAXN],ver1[MAXN],nex1[MAXN];
bitset<330>b[MAXN];
int q[MAXN],w[MAXN];
struct wy{int x,y;}t[MAXN],g[MAXN];
inline void add(int x,int y)
{
	ver[++len]=y;
	nex[len]=lin[x];
	lin[x]=len;
}
inline void add1(int x,int y)
{
	ver1[++len]=y;
	nex1[len]=lin1[x];
	lin1[x]=len;
	++w[y];
}
inline void dfs(int x)
{
	s[++top]=x;low[x]=dfn[x]=++cnt;
	go(x)
	{
		if(!dfn[tn])
		{
			dfs(tn);
			low[x]=min(low[x],low[tn]);
		}
		else if(!c[tn])low[x]=min(low[x],dfn[tn]);
	}
	if(dfn[x]==low[x])
	{
		int y=0;
		++id;
		while(y!=x)
		{
			y=s[top--];
			c[y]=id;
		}
	}
}
inline void topsort()
{
	int l=0,r=0;
	rep(1,id,i){if(!ru[i])q[++r]=i;}
	while(++l<=r)
	{
		int x=q[l];
		for(int i=lin1[x];i;i=nex1[i])
		{
			int tn=ver1[i];
			b[tn]=b[tn]|b[x];
			--ru[tn];
			if(!ru[tn])q[++r]=tn;
		}
	}
}
inline int cmp(wy a,wy b){return a.y<b.y;}
int main()
{
	freopen("1.in","r",stdin);
	//freopen("1.out","w",stdout);
	get(n);get(m);
	rep(1,m,i)
	{
		int x,y;
		get(x);get(y);
		t[i]=(wy){x,y};
		add(x,y);
	}
	rep(1,n,i)if(!dfn[i])dfs(i);
	len=0;
	rep(1,n,j)
	{
		go(j)
		{
			if(c[tn]==c[j])continue;
			add1(c[tn],c[j]);
		}
	}
	int B=(int)sqrt(1.0*id)+1;
	int ww=(id-1)/B+1;
	get(Q);
	rep(1,Q,i)
	{
		int get(x);int get(y); 	
		x=c[x];y=c[y];
		g[i]=(wy){x,y};
	}
	sort(g+1,g+1+Q,cmp);
	int flag=1;
	rep(1,ww,i)
	{
		int L=(i-1)*B+1;
		int R=min(n,i*B);
		rep(L,R,j)b[j][j]=1;
		topsort();
		while(g[flag].y<=R&&flag<=Q)
		{
			if(b[g[flag].x][g[flag].y]){puts("NO");return 0;}
			++flag;
		}
		if(flag==Q+1)break;
		rep(1,n,i)b[i].reset(),ru[i]=w[i];
	}
	puts("YES");
	put(m);
	rep(1,m,i)printf("%d %d\n",t[i].x,t[i].y);
	return 0;
}

原文：https://www.cnblogs.com/chdy/p/12691114.html