2.机器学习相关数学基础

1）贴上视频学习笔记，要求真实，不要抄袭，可以手写拍照。

一、概率论与贝叶斯先验

1. 本福特定律，又称第一数字定律，是指在实际生活得出的一组数据中，以1为首位数字出现的概率约为总数的三成;是直观想象1/9的三倍。

2.Nagel-Schreckenberg模型模拟

3.概率公式

条件概率：

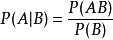
全概率公式：

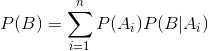
贝叶斯公式：

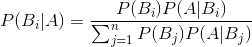
4.贝叶斯公式详解：

5.分布种类：

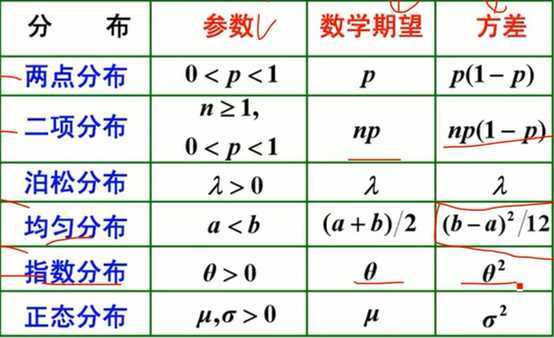
6.方差：

7.协方差

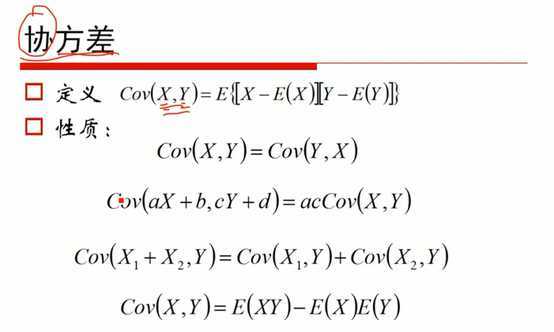
协方差的意义：

协方差是两个随机变量具有相同方向变化趋.势的度量;

若Cov(X,Y)>0，它们的变化趋势相同;

若Cov(X,Y)<0，它们的变化趋势相反;

若Cov(X,Y)=0，称X和Y不相关。

8.期望的性质

二、矩阵和线性代数

1.SVD(奇异值分解)

2.线性代数定义:

方阵的行列式

①1阶方 阵的行列式为该元素本身

②n阶方 阵的行列式等于它的任一行(或列)的各元

素与其对应的代数余子式乘积之和。

3.矩阵的乘法

A为m*s阶的矩阵，B为s*n阶的矩阵，那 么，C=A*B是m*n阶的矩阵，

其中,

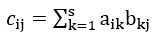
4.行列式

5.伴随矩阵

6.QR分解

7.向量的导数：A为m*n的矩阵，x为n*1的列向量，则Ax为m*1的列向量，记

8.总结

2）用自己的话总结“梯度”，“梯度下降”和“贝叶斯定理”

梯度：在向量微积分中，标量场的梯度是一个向量场。标量场中某一点上的梯度指向标量场增长最快的方向，梯度的长度是这个最大的变化率。

梯度下降：函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数之变化最快的方向。

贝叶斯定理：事件A在事件B已经发生的条件下的概率，与事件B在事件A已经发生的条件下的概率不同，但是两者的概率是相关的。

　　　　　　　　贝叶斯公式： P(A|B) = P(A) * [P(B|A)/P(B)] 

P(A|B)会随着P(A)和P(B|A)的增长而增长，随着P(B)的增长而减少。

原文：https://www.cnblogs.com/zqy1004/p/12690120.html