深度学习（四）：马尔科夫链蒙特卡洛采样（MCMC）

一、引入

拒绝采样，重要性采样的效率在高维空间很低，随维度增长其难度指数型增长，主要适用于一维的采样。对于二维以上可以用马氏链。马尔可夫链蒙特卡洛采样方法就是在高维空间采样的方法。

马尔可夫链就是满足马尔可夫假设的一组状态序列\left \{ x_{t} \right \}= ...,x_{t-2}, x_{t-1}, x_{t}, x_{t+1},...，其中假设某一时刻状态x_{t}发生状态转移的概率只依赖于它的前一个状态x_{t-1}，这个就是马尔可夫假设：

P(X_{t+1}\mid X_{t-2}, X_{t-1}, X_{t}, X_{t+1} )=P(X_{t+1}\mid X_{t})

只要我们能知道系统中任意两个状态之间的转移概率，整个马尔可夫模型就知道了，定义转移概率为：

P_{ij}=P(X_{t+1}=j\mid X_{t}=i)

转移概率衡量的是两个状态之间的转移几率，与时刻无关，仅涉及相邻的两个状态，如果系统中的状态有T种，那么转移概率可以构成一个T×T的转移矩阵P，马尔可夫链有收敛性质，就是说从任意一个初始分布出发，经过多次转移后，得到的分布是平稳的，不再变化的分布q，这个平稳分布q与初始分布无关，只与状态转移矩阵P有关，接下来用一段代码说明这个问题：

matrix1=np.matrix([[0.9,0.075,0.025],[0.15,0.8,0.05],[0.25,0.25,0.5]],dtype=float)
vector1=np.matrix([[0.3,0.4,0.3]],dtype=float)
for i in range(100):
  vector1=vector1*matrix1
  print(‘current round:‘,i+1)
  print(vector1)

输出最开始定义的matrix1和vector1，分别是转移概率和初始概率分布：

初始概率分布vector1表示的是在t=0时刻，P(X_{0}=0)=0.3，P(X_{0}=1)=0.4，P(X_{0}=2)=0.3，描述的是起初时刻，状态的分布情况，这里默认有三种状态，分别是1,2,3。

转移矩阵matrix1的位置11上的元素0.9表示的是：当前一时刻的状态X_{t-1}取1时，下一时刻的状态X_{t}取1的概率为0.9；

位置12上的元素0.075表示的是：当前一时刻的状态X_{t-1}取1时，下一时刻的状态X_{t}取2的概率为0.075；

可以用vector1*matrix1用矩阵乘法公式来计算一下，会得到一个形式和vector1一样的矩阵，有三个元素，每个元素表示的就是该时刻的状态分布情况：

根据矩阵乘法公式来计算一下下一时刻的状态分布的第一个元素为：（0.3*0.9+0.4*0.15+0.3*0.25），可以看出，它表示的是【不管上一时刻是取了哪个值，下一时刻状态为1的概率】，这个元素的计算考虑了上一个时刻的状态分布概率，比如0.3*0.9，这个乘积的含义就是上一时刻状态为1的概率是0.3，在上一时刻状态为1的条件下下一时刻状态仍为1的概率是0.9，注意这里的0.9是个条件概率；相乘就可以得到上一时刻状态为1，且下一时刻状态为1的概率，这里注意这是个联合概率分布。

输出一下整体的代码结果：

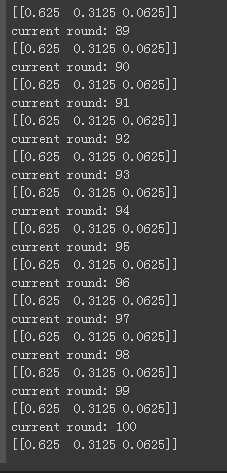
我们发现最后得到的分布基本是平稳不变的，即：状态取0和3的概率是0.625，状态取1的概率是0.3125。我们可以改变初始vector1，但是最终收敛的平稳分布依旧是不变的。这个就是马氏链的收敛。

我们的目标是希望从平稳分布q中进行采样。现在的问题如下：

• 什么样的马氏链可以收敛到一个平稳分布q？所有的马氏链都收敛吗？
• 既然q只和转移矩阵P有关，我们一开始要如何确定马氏链中的转移矩阵P，使得平稳分布是我们想要的q？
• 马氏链收敛到平稳分布的速度快吗？怎么样的马氏链可以快速收敛到q？
• 如果我们找到了目标平稳分布所对应的转移矩阵P，我们具体要怎么从平稳分布中采样？

原文：https://www.cnblogs.com/liuxiangyan/p/12569113.html