【数据结构】线段树 (区间修改/区间求和)
【本文解决 区间修改/区间求和 的问题】
区间求和部分内容与上一篇内容相同,详见 线段树点修改/区间求和
已经知道了在O(logN)的复杂度内求N个连续数之和的做法
对于区间修改,最简单的办法就是进行多次点修改
但是多次点修改最后的时间复杂度为O(NlogN),还不及最普通的数组模拟O(n)效率高
并且,多次点修改的操作与用树状数组模拟几乎无差别,甚至说树状数组写起来要比线段树简单得多
所以对于区间修改,要引入一种叫做“懒惰标记”的概念
进行区间标记时的线段树节点结构体定义方式
struct node
{
int l,r;
ll sum,lazy;
void add(ll x)
{
sum+=x*(r-l+1);
lazy+=x;
}
}tree[MAXN*4];懒惰标记的添加方法
如果当前要把 [L,R] 这一整个区间内的每个元素加上x
与点修改的方式相同,从根节点开始向下寻找
关键:如果找到一个节点,它表示的线段完全包含于 [L,R] 的话,不需要继续修改它的子树,而是直接在这个节点上进行懒惰标记即可(即在这个节点包含着的所有叶子节点的公共祖先上标记)
标记方法为:这个节点的sum值加上节点表示的区间内的元素个数乘以x,并将lazy值加上x
即上述代码中的add函数
懒惰标记添加图示
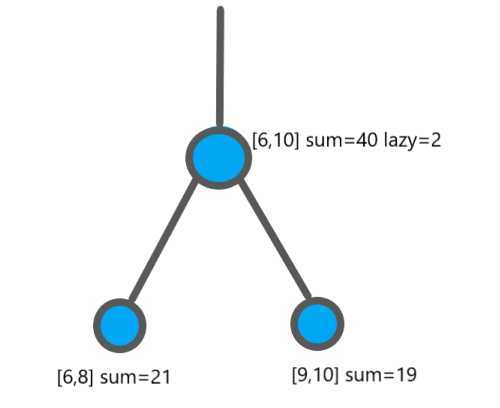
如上图所示,假设有个长度为10的序列,初始值分别为1~10
即6~10和为40,6~8和为21,9~10和为19
此时有一个操作,要将6~10之间所有元素增加2
发现此时这个节点表示的线段[6,10]正好在要求的范围内
此时不需要继续寻找下去给每个叶子节点加2然后再回溯
只需要在当前这个节点上给懒惰标记lazy +2即可
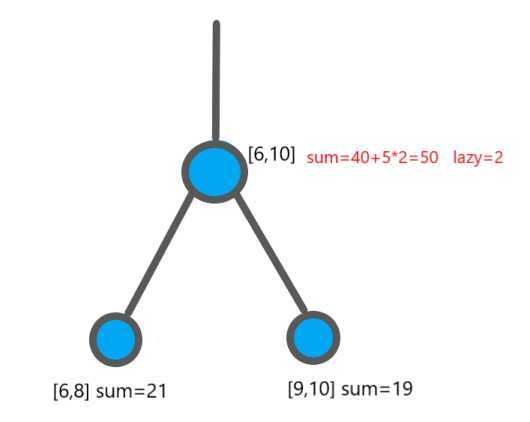
懒惰标记在查询中的变化与作用
接着上述图示中的例子
假设添加完懒惰标记后要查找[8,10]之间的元素之和
同样的,根据上一篇的方法来到[6,10]这个节点,发现[8,10]包含于[6,10]
此时就需要进行一个操作——向下传递懒惰标记 push_down
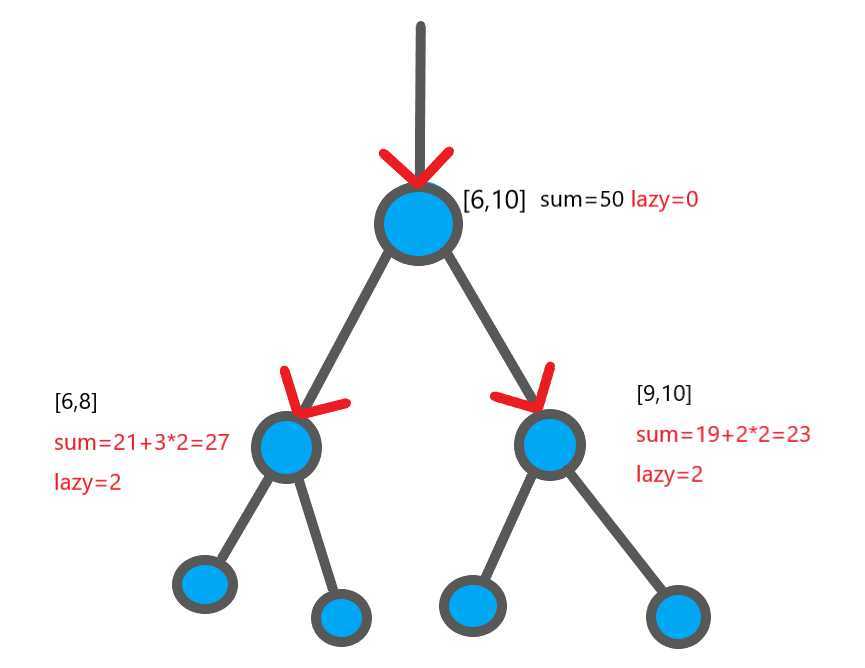
传递后的结果如图所示,然后再往下寻找答案
先考虑左儿子,[6,8]与[8,10]有部分重叠,说明这个节点的子树里存在某个节点对答案有贡献
所以继续向下传递懒惰标记
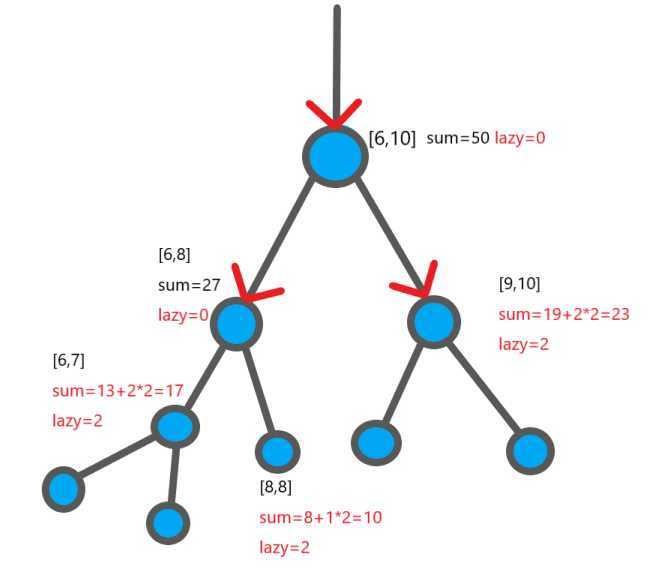
左节点表示的线段[6,7]与查询区间无交点,舍去
发现右节点完全包含于[8,10],所以返回[8,8]这个节点的值10
这样[6,10]的左子树查找完毕,看右节点
发现右节点[9,10]完全包含于[8,10],所以此时不需要向下传递,直接返回sum值23
查找完成,答案为10+23=33
懒惰标记的总结
从几幅图中可以很明显的看到,懒惰标记是只有在要使用的时候才会向下传递,而在没有明确使用时只会标记在区间的公共祖先上
如果非叶子节点表示的线段完全满足查询要求,直接返回节点的sum值即可
如果非叶子节点表示的线段完全不满足查询要求,说明整个子树都不满足,也不需要向下传递
只有在非叶子节点表示的线段部分满足查询要求,说明这个节点的sum值虽然不能直接使用,但是节点的子树内会有节点需要使用,此时再进行向下传递
这也是这种标记被叫做懒惰的由来——用的时候再说
代码实现部分
向下传递 push_down
void push_down(int id) { tree[id<<1].add(tree[id].lazy); tree[id<<1|1].add(tree[id].lazy); tree[id].lazy=0; }即把id节点的lazy值传给两个子节点,同时id节点的lazy值清零
建树 buildTree
void buildTree(int id,int l,int r) { tree[id].l=l; tree[id].r=r; tree[id].sum=tree[id].lazy=0; if(l==r) tree[id].sum=ar[l]; else { int mid=(l+r)>>1; buildTree(id<<1,l,mid); buildTree(id<<1|1,mid+1,r); push_up(id); } }相对于点修改的建树
这里只是多了一句
tree[id].lazy=0而已更新 update
void update(int id,int l,int r,ll val) { int L=tree[id].l,R=tree[id].r; if(l<=L&&R<=r) tree[id].add(val); else { push_down(id); int mid=(L+R)>>1; if(mid>=l) update(id<<1,l,r,val); if(mid<r) update(id<<1|1,l,r,val); push_up(id); } }如果访问到的id节点所表示的线段完全包含于查询区间[l,r]的话
只需要直接往id节点打上懒惰标记即可
否则,需要先向下传递懒惰标记,再对子节点进行更新,最后回溯更新自身
如果不先向下传递标记,会在回溯时因为没有处理懒惰标记就更新sum值导致错误
查询 query
ll query(int id,int l,int r) { int L=tree[id].l,R=tree[id].r; if(l<=L&&R<=r) return tree[id].sum; push_down(id); int mid=(L+R)>>1; ll res=0; if(mid>=l) res+=query(id<<1,l,r); if(mid<r) res+=query(id<<1|1,l,r); push_up(id); return res; }如果此时id表示的区间完全包含于查询的区间,直接返回sum值即可
否则,向下传递懒惰标记,再以两个子节点返回的值作为答案即可
完整程序
以 POJ 3468 的输入样式为例
C a b c 将[a,b]之间的值增加c
Q a b 查询[a,b]之和
#include<iostream>
using namespace std;
typedef long long ll;
const int MAXN=1e5+50;
struct node
{
int l,r;
ll sum,lazy;
void add(ll x)
{
sum+=x*(r-l+1);
lazy+=x;
}
}tree[MAXN*4];
int ar[MAXN];
void push_up(int id)
{
tree[id].sum=tree[id<<1].sum+tree[id<<1|1].sum;
}
void push_down(int id)
{
tree[id<<1].add(tree[id].lazy);
tree[id<<1|1].add(tree[id].lazy);
tree[id].lazy=0;
}
void buildTree(int id,int l,int r)
{
tree[id].l=l;
tree[id].r=r;
tree[id].sum=tree[id].lazy=0;
if(l==r)
tree[id].sum=ar[l];
else
{
int mid=(l+r)>>1;
buildTree(id<<1,l,mid);
buildTree(id<<1|1,mid+1,r);
push_up(id);
}
}
void update(int id,int l,int r,ll val)
{
int L=tree[id].l,R=tree[id].r;
if(l<=L&&R<=r)
tree[id].add(val);
else
{
push_down(id);
int mid=(L+R)>>1;
if(mid>=l)
update(id<<1,l,r,val);
if(mid<r)
update(id<<1|1,l,r,val);
push_up(id);
}
}
ll query(int id,int l,int r)
{
int L=tree[id].l,R=tree[id].r;
if(l<=L&&R<=r)
return tree[id].sum;
push_down(id);
int mid=(L+R)>>1;
ll res=0;
if(mid>=l)
res+=query(id<<1,l,r);
if(mid<r)
res+=query(id<<1|1,l,r);
push_up(id);
return res;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int i,n,q,a,b,d;
char opr[5];
cin>>n>>q;
for(i=1;i<=n;i++)
cin>>ar[i];
buildTree(1,1,n);
while(q--)
{
cin>>opr;
if(opr[0]=='Q')
{
cin>>a>>b;
cout<<query(1,a,b)<<'\n';
}
else
{
cin>>a>>b>>d;
update(1,a,b,d);
}
}
return 0;
}原文:https://www.cnblogs.com/stelayuri/p/12526469.html
