1. AMORE

1.1 newff

newff(n.neurons, learning.rate.global, momentum.global, error.criterium, Stao, hidden.layer, output.layer, method)

• n.neurons：包含每层神经元的数值向量。第一个元素是输入神经元的数量，最后一个元素是输出神经元的数量，剩余的是隐含层神经元的数量；
• learning.rate.global：每个神经元训练时的学习效率；
• momentum.global：每个神经元的动量，仅几个训练算法需要该参数；
• error.criterium：用于度量神经网络预测目标值接近程度的标准，可以使用以下几项：

  "LMS"：Least Mean Squares

  "LMLS"：Least Mean Logarithm Squared

  "TAO"：TAO Error

• Stao：当上一项为TAO时的Stao参数，对于其他的误差标准无用
• hidden.layer：隐含层神经元的激活函数，可用："purelin"、"tansig"、"sigmoid"、"hardlim"、"custom"，其中"custom"表示需要用户自定义神经元的f0和f1元素；
• output.layer：输出层神经元的激活函数；
• method：优先选择的训练方法，包括：

  "ADAPTgd": Adaptative gradient descend.（自适应的梯度下降方法）
  "ADAPTgdwm": Adaptative gradient descend with momentum.（基于动量因子的自适应梯度下降方法）
  "BATCHgd": BATCH gradient descend.（批量梯度下降方法）
  "BATCHgdwm": BATCH gradient descend with momentum.（基于动量因子的批量梯度下降方法）

1.2 train

train(net, P, T, Pval=NULL, Tval=NULL, error.criterium="LMS", report=TRUE, n.shows, show.step, Stao=NA, prob=NULL, n.threads=0L)

• net：要训练的神经网络；
• P：训练集输入值；
• T：训练集输出值；
• Pval：验证集输入值；
• Tval：验证集输出值；
• error.criterium：度量拟合优劣程度的标准；
• Stao：用于TAO算法的参数初始值；
• report：逻辑值，是否打印训练过程信息；
• n.shows：当上一项为TRUE时，打印的总次数；
• show.step：训练过程一直进行到函数允许打印报告信息时经历的迭代次数；
• prob：每一个样本应用到再抽样训练时的概率向量；
• n.threads：用于BATCH*训练方法的线程数量，如果小于1，它将产生NumberProcessors-1个线程，其中NumberProcessors为处理器的个数，如果没有找到OpenMP库，该参数将被忽略。

1.3 example

library(AMORE)
# P is the input vector
P <- matrix(sample(seq(-1,1,length=1000), 1000, replace=FALSE), ncol=1) 
# The network will try to approximate the target P^2
target <- P^2                                   
# We create a feedforward network, with two hidden layers.
# The first hidden layer has three neurons and the second has two neurons.
# The hidden layers have got Tansig activation functions and the output layer is Purelin.
net <- newff(n.neurons=c(1,3,2,1), learning.rate.global=1e-2, momentum.global=0.5,
        error.criterium="LMS", Stao=NA, hidden.layer="tansig", 
        output.layer="purelin", method="ADAPTgdwm")
result <- train(net, P, target, error.criterium="LMS", report=TRUE, show.step=100, n.shows=5 )
P_test <- matrix(sample(seq(-1,1,length=1000), 100, replace=FALSE), ncol=1)
target_test <- P_test^2
y_test <- sim(result$net, P_test)
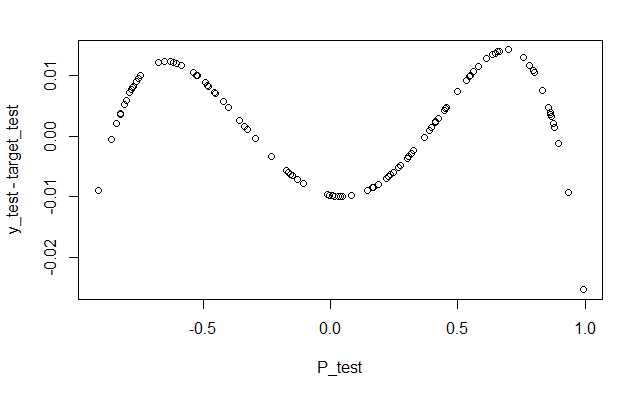
plot(P_test,y_test-target_test,lty=1)

index.show: 1 LMS 0.0893172434474773
index.show: 2 LMS 0.0892277761187557
index.show: 3 LMS 0.000380711026069436
index.show: 4 LMS 0.000155618390342181
index.show: 5 LMS 9.53881309223154e-05

1.4 exercise

原文：https://www.cnblogs.com/dingdangsunny/p/12325437.html