第三周：超参数调试 、 Batch 正则化和程序框架（Hyperparameter tuning）

3.1 调试处理（Tuning process）

调整超参数，如何选择调试值：

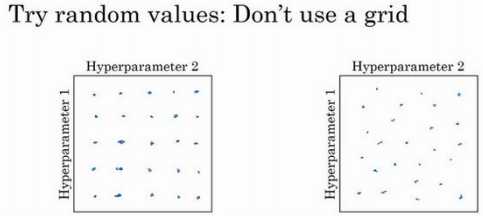
实践中，搜索的可能不止三个超参数，很难预知哪个是最重要的超参数，随机取值而不是网格取值表明，探究了更多重要超参数的潜在值。

另一个惯例是采用由粗糙到精细的策略：

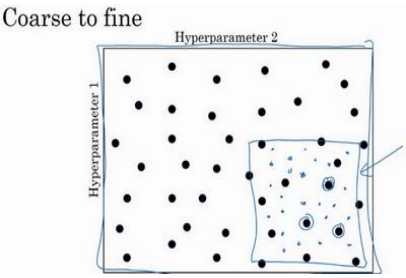
在整个的方格中进行粗略搜索后，接下来聚焦到更小的方格中。在更小的方格中，可以更密集的取点。

3.2 为超参数选择合适的范围（Using an appropriate scale to pick hyperparameters）

假设在搜索超参数??（学习速率），假设怀疑其值最小是 0.0001 或 最大是 1。如果画一条从 0.0001 到 1 的数轴，沿其随机均匀取值，那 90%的数值将会落在0.1 到 1 之间，结果就是，在 0.1 到 1 之间，应用了 90%的资源，而在 0.0001 到 0.1 之间， 只有 10%的搜索资源。

用对数标尺搜索超参数的方式会更合理，因此这里不使用线性轴，分别依次取 0.0001，0.001，0.01，0.1，1，在对数轴上均匀随机取点。

在 Python 中，可以这样做，使 r=-4*np.random.rand()，然后??随机取值， \(?? = 10^??\)，所以，第一行可以得出?? ∈ [4,0]，那么?? ∈ [\(10^{?4}\) , 100 ]，所以最左边的数字是\(10^{?4}\)， 最右边是100。

另一个棘手的例子是给?? 取值，用于计算指数的加权平均值：

如果想在 0.9 到 0.999 区间搜索，不要随机均匀在此区间取值，考虑这个问题最好的方法就是，探究的是1 ? ??，此值在 0.1 到 0.001 区间内。

设定了\(1 ? ?? = 10^??\)，所以\(?? = 1 ? 10^??\)，然后这就变成了在特定的选择范围内超参数随机取值。

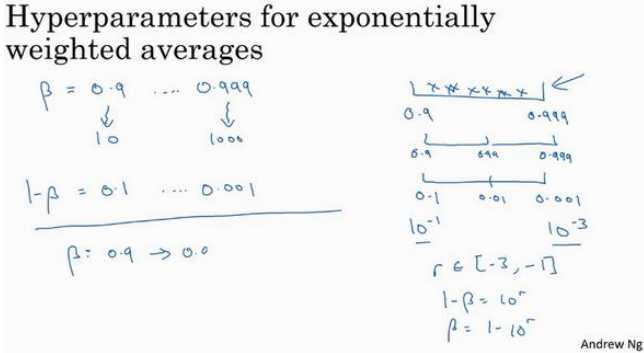
当??接近 1 时，??就会对细微的变化变得很敏感。所以整个取值过程中，需要更加密集地取值。

3.3 超参数调试实践：Pandas VS Caviar（Hyperparameters tuning in practice: Pandas vs. Caviar）

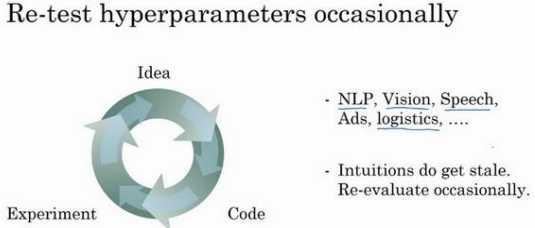
这两种方式的选择，是由拥有的计算资源决定的。

3.4 归一化网络的激活函数（Normalizing activations in a network）

Batch 归一化是怎么起作用的：

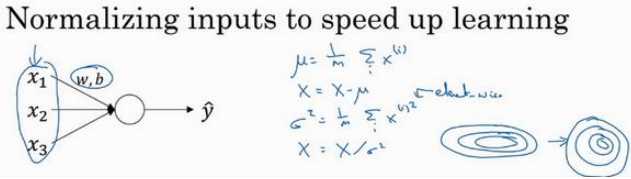
训练一个模型，比如 logistic 回归时，归一化输入特征可以加快学习过程。

更深的模型，实践中，经常做的是归一化，对每一层的z值标准化，化为含平均值 0 和标准单位方差，??的每一个分量都含有平均值 0 和方差 1，但不想让隐藏单元总是含有平均值 0 和方差 1，也许隐藏单元有了不同的分布会有意义，所以要做的就是计算，\(，\widetilde{z}^{(??)}，\widetilde{z}^{(??)} = \gamma??_{norm}^{ (??)} + \beta\) 这里??和??是 模型的学习参数，之后会使用梯度下降或一些其它类似梯度下降的算法， 比如 Momentum 或者 Nesterov，Adam，更新??和??，正如更新神经网络的权重一样。

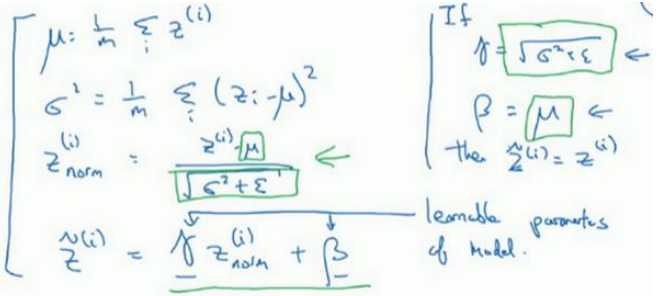
注意??和??的作用：如果\(\gamma = \sqrt{\sigma^2+\epsilon}\) ，\(\beta=\mu\)，则\(z^{(i)}_{norm}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^2}+\epsilon}\) , \(\widetilde{z}^{(??)} = \gamma??_{norm}^{ (??)} + \beta\) ，\(\widetilde{z}^{(??)}=z^{(i)}\) 。通过对??和??合理设定，规范化过程，通过赋予??和??其它值，可以构造含其它平均值和方差的隐藏单元值。

Batch 归 一化的作用是它适用的归一化过程，不只是输入层，甚至同样适用于神经网络中的深度隐藏 层。

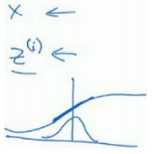
如果有 sigmoid 激活函数，不想让数值总是全部集中在线性这里，想使它们有更大的方差，或不是 0 的平均值，以便更好的利用非线性的 sigmoid 函数，而不是使所有的值都集中于这个线性版本中，有了??和??两个参数后，学习算法可以设置为任何值，而不仅仅局限于0-1之间。

3.5 将 Batch Norm 拟合进神经网络（Fitting Batch Norm into a neural network）

Batch 归一化的做法是将\(??^{[l]}\) 值进行 Batch 归一化，简称 BN，此过程将由\(??^{[l]}\)和\(??^{[l]}\)两参数控制，这一操作会给一个新的规范化的 \(??^{[l]}\) 值（\(\widetilde{z}^{[1]}\)），然后将其输入激活函数中得到\(??^{[l]}\)，即\(??^{[l]} = ??^{[l] }(\widetilde{z}^{ [??]} )\)。

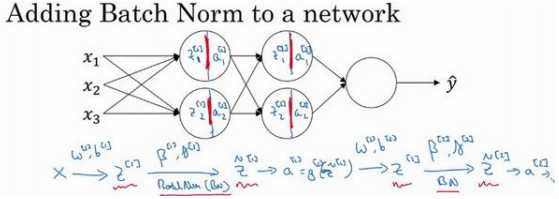
Batch 归一化是发生在计算??和??之间的。接下来可以使用想用的任何一种优化算法，比如梯度下降法来执行它。 举个例子，对于给定层，计算\(????^{ [??]}\)，接着更新参数??为\(??^{[??]} = ??^{[??]} ? ??????^{[??]}\)对于??也是如此\(??^{[??]} = ??^{[??]} ? ??????^{[??]}\)。。也可 以使用 Adam 或 RMSprop 或 Momentum，以更新参数??和??，并不是只应用梯度下降法。

在 TensorFlow 框架中，可以用函数（tf.nn.batch_normalization）来实现 Batch 归一化

如果使用 Batch 归一化，可以消除参数（\(??^{[??]}\)），或者 也可以， 暂时把它设置为 0，那么，参数变成\(??^{[??]} = ??^{[??]}??^{[???1]}\),最后会用参数\(??^{[??]}\)，以便决定\(\widetilde{z}^{[??]}\)的取值。

在 Batch 归一化的过程中，计算\(??^{[??]}\)的均值，再减去平均值，这意味着，无论\(??^{[??]}\) 的值是多少，都是要被减去的。

最后，请记住\(??^{[??]}\)的维数，因为在这个例子中，维数会是\((??^{[??]} , 1)\)，\(??^{[??]}\)的尺寸为\((??^{[??]} , 1)\)， 如果是 l 层隐藏单元的数量，那\(??^{[??]}\)和\(??^{[??]}\)的维度也是\((??^{[??]} , 1)\)，因为这是隐藏层的数量，有\(??^{[??]}\)隐藏单元，所以\(??^{[??]}\)和\(??^{[??]}\)用来将每个隐藏层的均值和方差缩放为网络想要的值。

3.6 Batch Norm 为什么奏效？（Why does Batch Norm work?）

一个原因是，归一化输入特征值??，使其均值为 0，方差 1，通过归一化所有的输入特征值 ??，以获得类似范围的值，可以加速学习。

Batch 归一化有效的第二个原因是，它可以使权重比网络更滞后或更深层：

Batch 归一化减少了输入值改变的问题，它使这些值变得更稳定，神经网络的之后层有更坚实的基础。即使输入分布改变了一些，它会改变得更少。它做的是当前层保持学习，当改变时，迫使后层适应的程度减小了，可以这样想，它减弱了前层参数的作用与后层参数的作用之间的联系，它使得网络每层都可以自己学习，稍稍独立于其它层，这有助于加速整个网络的学习。

Batch 归一化还有一个作用，它有轻微的正则化效果：

Batch 归一化含几重噪音，因为标准偏差的缩放和减去均值带来的额外噪音。类似于 dropout，Batch 归一化有轻微的正则化效果，因为给隐藏单元添加了噪音，这迫使后部单元不过分依赖任何一个隐藏单元， 类似于 dropout，它给隐藏层增加了噪音，因此有轻微的正则化效果。因为添加的噪音很微小，所以并不是巨大的正则化效果。

3.7 测试时的 Batch Norm（Batch Norm at test time）

Batch 归一化将数据以 mini-batch 的形式逐一处理，但在测试时，需要对每个样本逐一处理：

在测试时，可能不能将一个 mini-batch 中的 6428 或 2056 个样本同时处理，因此需要用其它方式来得到?? 和\(??^2\)，而且如果只有一个样本，一个样本的均值和方差没有意义。那么实际上，为了将神经网络运用于测试，就需要单独估算??和\(??^2\)，在典型的 Batch 归一化运用中，需要用一个指数加权平均来估算，这个平均数涵盖了所有 mini-batch：

可以用指数加权平均来追踪在某一层的第一个 mini-batch 中所见的\(\mu,??^2\)的值，以及第二个 mini-batch 中所见的\(\mu,??^2\)的值等等。最后在测试时，对应这个等式\(（）（??_{norm}^{ (??)} = \frac{??^{ (??)}???}{\sqrt{??^2+??}} ）\)，只需要用??值来计算\(??_{norm }^{(??)}\) ，用 ??和\(??^2\)的指数加权平均。

总结一下就是，在训练时，??和\(??^2\)是在整个 mini-batch 上计算出来的包含了像是 64 或 28 或其它一定数量的样本，但在测试时，需要逐一处理样本，方法是根据训练集估算??和\(??^2\)，估算的方式有很多种，理论上可以在最终的网络中运行整个训练集来得到 ??和\(??^2\)，但在实际操作中，通常运用指数加权平均来追踪在训练过程中看到的??和\(??^2\) 的值。然后在测试中使用 ??和\(??^2\)的值来进行所需要的隐藏单元??值的调整。

3.8 Softmax 回归（Softmax regression）

3.9 训练一个 Softmax 分类器（Training a Softmax classifier）

Softmax 这个名称的来源是与所谓 hardmax 对比，hardmax 会把向量??变成向量\(\left[ \begin{matrix}1\\0\\0\\0 \end{matrix}\right]\)， hardmax 函数会观察??的元素，然后在??中最大元素的位置放上 1，其它位置放上 0。

怎样训练带有 Softmax 输出层的神经网络：

在 Softmax 分类中，我们一般用到的损失函数是 $ ??(\hat{??} , ??) = ?\sum_{j=1}^4 ??_?? ?????? \hat{??}_j\(,因为梯度下降法是用来减少训练集的损失的，要使它变小的唯一方式就是使\)?log \hat{??}_2\(变小，要想做到这一点，就需要使\)??_2$尽可能大， 因为这些是概率，所以不可能比 1 大。整个训练集的损失J：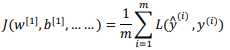

因此要做的就是用梯度下降法，使这里的损失最小化。

在有 Softmax 输出层时如何实现梯度下降法，关键方程是这个表达式\(????^{[??]} = \hat{??} ? y\) 具体推导：

softmax交叉熵损失函数求导

3.10 深度学习框架（Deep Learning frameworks）

3.11 TensorFlow

tensorflow 基础使用，教程网上很多，自查。

原文：https://www.cnblogs.com/phoenixash/p/12129233.html