数据探索

1,数据质量分析

• 数据质量分析是数据挖掘中数据准备环节中的重要一环,是数据预处理的前提,也是数据挖掘分析结论有效性和准确性基础,没有可信的数据,数据挖掘构建的模型将是空中楼阁
• 数据质量分析的主要任务时检查原始数据中是否存在脏数据,脏数据一般是指不符合要求,以及不能直接进行相应的分析的数据。脏数据一般包括:
  • 缺失值
  • 异常值
  • 不一致的值
  • 重复数据及含有特殊符号(如#、¥、*)的数据

2,缺失值分析

• 数据的缺失值主要包括记录的缺失和记录中某个字段信息的缺失,原因两者丢回熬成分析结果的不准确

缺失值产生的原因

1. 有些信息暂时无法获取,或者获取信息的代价太大
   1. 有些信息是被遗漏的。可能是因为输入时认为不重要、忘记填写或对数据理解错误等一些认为因素而遗漏,也可能由于数据采集设备的故障、存储介质的故障、传输媒体的故障灯非认为原因而丢失。再某些情况下,缺失值并不意味着
   2. 属性值不存在。在某些情况下,缺失值并不意味着数据有错误。对一些对象来说,某些属性值是不存在的,如一个未婚者的配偶姓名、一个儿童的固定收入等
2. 缺失值的影响
   1. 数据挖掘建模将丢失大量的有用信息
   2. 数据挖掘模型所表现出的不确定性更加显著,模型中蕴含的规律更难把握
   3. 包含空值的数据会使建模过程陷入混乱,导致不可靠的输出
3. 缺失值的分析
   • 使用鉴定单的统计分析,可以得到含有缺失值的树脂字那个的个数,以及每个属性的未缺失数,缺失数与缺失率等
   • 总体来说,缺失值的处理分为删除存在缺失值的记录、对可能进行插补和不处理3中情况

3,异常值的分析

• 异常值的分析是检验数据是否有录入错误以及含有不合常理的数据,护士异常值的存在是十分危险的,不加剔除地把异常值包括进数据的计算分析过程中,对结果会产生不良的影响,重视异常值的出现,分析其产生的原因,常常,成为发现问题进而改进决策的契机
• 异常值是指样本中的个别值,其数值明显偏离其余的观测值。异常值也称为离群点,异常值的分析也称为离群点分析

1. 简单统计量分析
   • 可以先对变量做一个描述性统计,进而查看那些数据是不合理的。最常用的统计量是最大值和最小值,用来判断这个变量的取值是否超出了合理的范围
2. 3σ原则
   
   • 如果数据服从正太分布,在3σ原则下,异常值被定义为一组测定值中与平均值偏差超过3被标准差的值。在正太分布假设下,距离平均值3σ之外的值出现的概率为p(|x-μ|>3σ)<=0.003,属于极个别的小概率事件,如果不服从正态分布,也可以用远离平均值的多少倍标准差来描述
3. 箱形图分析
   • 箱型图提供了是被异常值的标准:异常值通常被定义为小于Q_L-1.5IQR或大于Q_U+1.5IQR的值。Q_L称为下四分位数,表示全部观察值中有四分之一的数据取值比它小;Qu称为上四分位数,表示全部观察值中有四分之一数据 取值比它大;IQR称为四分位数间距,是上分位数Qu与下分位数Q_L之差,其间包含了全部观察值的一半
   • 箱型图依据实际数据绘制,没有对数据作3任何限制性要求(如服从某种特定分布形式),它只是真实直观的表现数据分布的本来面貌;另一方面,箱型图判断异常值的标准以四分位数和四分位间距为基础,四分位数具有一定的鲁棒性;多达25%的数据可以变得任意远而不会很大的扰动四分位数,所以异常值不能对这个标准施加影响。由此可见,箱型图识别异常值的结果比较客观,在识别异常值有一定的优势。
   • 鲁棒性:鲁棒是Robust的音译，也就是健壮和强壮的意思。它是在异常和危险情况下系统生存的关键。比如说，计算机软件在输入错误、磁盘故障、网络过载或有意攻击情况下，能否不死机、不崩溃，就是该软件的鲁棒性。所谓“鲁棒性”，是指控制系统在一定（结构，大小）的参数摄动下，维持其它某些性能的特性。根据对性能的不同定义，可分为稳定鲁棒性和性能鲁棒性。以闭环系统的鲁棒性作为目标设计得到的固定控制器称为鲁棒控制器。

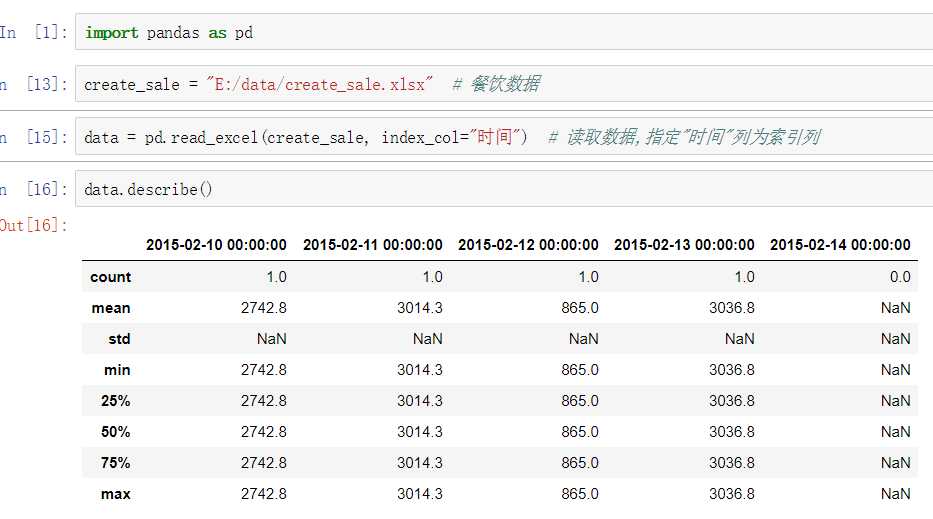
• 参数说明:
  • count是非空值数,通过len(data)可以知道数据记录为若干条,因此缺失值为1
• 异常值检测代码:

import pandas as pd
create_sale = "E:/data/create_sale.xlsx"
data = pd.read_excel(create_sale, index_col="时间")

import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"] = ["SimHei"]  # 用来显示正常的中文
plt.rcParams["axes.unicode_minus"] = False

plt.figure()  # 建立画像
p = data.boxplot()  # 画箱线图,直接使用Dataframe的方法
print(p)
x = p["fliers"][0].get_xdata()  #  "filers"即为异常值的标签
y = p["fliers"][0].get_ydata()
y.sort()  # 从小到大排序,该方法直接改变原对象

# 用annotate添加注释
# 其中有些相近的点,注释你会出现重叠,难以看清,需要一些技巧来控制
for i in range(len(x)):
    if i > 0:
        plt.annotate(y[i], xy=(x[i], y[i]), xytext=(x[i]+0.05 -0.8/(y[i]-y[i-1]), y[i]))
    else:
        plt.annotate(y[i], xy=(x[i], y[i]), xttext=(x[i]+0.08, y[i]))
plt.show()

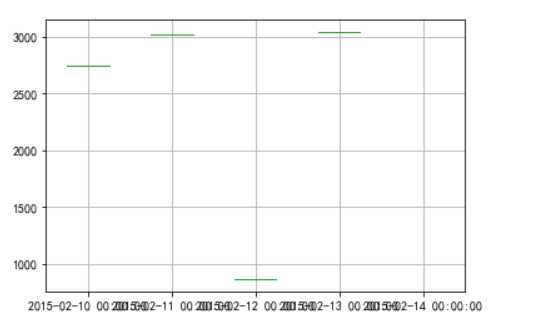
• 由于数据源有误图形,不够准确,当有值以后,结合具体业务去除异常数据,编写过滤程序

4,一致性分析

• 数据不一致性是指数据的矛盾性、不相容性。直接对不一致的数据进行挖掘,可能会产生与实际相违背的挖掘效果.
• 在数据挖掘过程中,不一致数据的产生主要发生在数据集成的过程中,这可能是由于被挖掘数据是来自于从不同的数据源、对于重复存放 的数据未能进行一致性更新造成的.列如(两张表中都存储了用户的电话号码,但是在用户的电话号码发生让那个改变时,只更新了一张表的数据,那么两张表中就有不一致的数据)

5,数据特征分析:

• 对数据进行质量的分析以后,接下来可通过绘制图表、计算某些特征量等手段进行数据的特征分析

1. 分布分析
   • 分布分析能揭示数据的分布特征和分布类型。对于定量数据,欲了解其分布形式是对称的还是非对称的,发现某些特大或特小的可疑值,可通过绘制频率分布表、绘制频率分布直方图、绘制茎叶图及进行直观的分析;对于定性分类数据,可用饼图和条形图直观地显示分布情况
1. 定量数据的分步分析
• 对于定量而言,选择"组数"和"组宽"是做频率分布分析有以下步骤:
  1. 求极差
  2. 决定组距与组数
  3. 决定分点
  4. 列出频率分布表
  5. 绘制频率分布直方图
• 遵循的主要原则如下
1. 各组之间必须是相互排斥的
2. 各组必须将所有的数据包含在内
3. 各组的组宽最好相等导入“捞起生鱼片”的销售数据，如下图：

1. 求极差
   • 极差=最大值-最小值=3960-45=3915
2. 分组
   • 这里根据业务数据的含义，可取组距为500
   • 组数=极差/组距=3915/500=7.83=》8
3. 决定分点
   • 分布区间如下：

原文：https://www.cnblogs.com/ljc-0923/p/10988394.html