记502 dp专练
趁着503的清早 我还算清醒把昨天老师讲的内容总结一下,昨天有点迷了 至使我A的几道题都迷迷糊糊的。(可能是我太菜了)


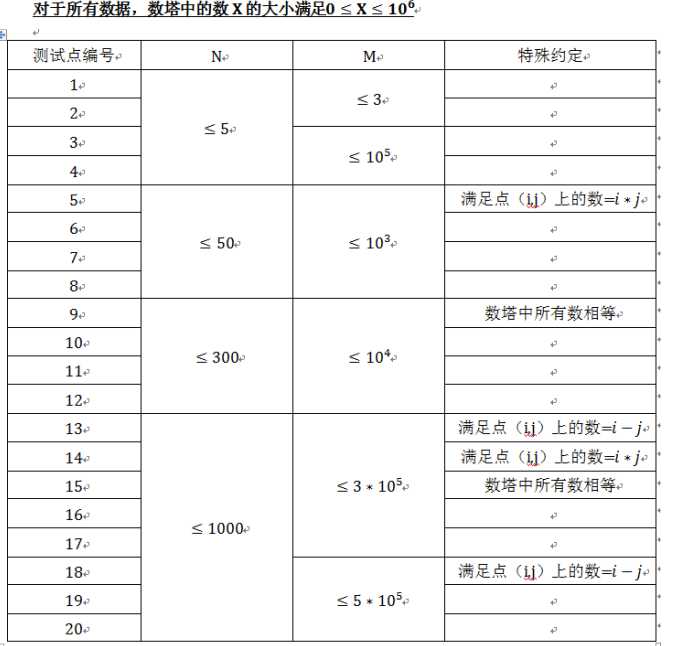
这道题显然是 数字三角形的变形 好没有经过认真思考然后直接暴力了 这是很不应该的 但正解 是需要你能深刻理解数字三角形的模板式究竟是什么含义这显然是我这种 感觉很简单的东西没有认真思考每一个f值所以造成这道题没有写出正解。
bf: 求出一条答案路径,如果询问在这条路径上那就直接暴力跑一遍不在的话直接输出最大值 复杂度n^3 实际低分很低貌似写挂了。
当然 100分的做法也很简单 我们只需考虑原本的f数组的含义表示右上到下到此点的最大的和。
对于一个答案显然是某一行中的一个点的由上到下和由下到上的和。 于是可以加一个数组g[i][j]表示右下到上的到达这个点的最大和。
显然 对于ban掉的一个点,不在1,1 那就不是-1 然后次大值是由 当前这行旁边的点构成的 那么我们再在当前这行再求一个次大值直接用f 和g数组求即可。解法就是这样了 对于每一行求出最大值 求出最大值 路径 求出次大值,询问输出即可。n^2

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cmath> #include<cstdio> #include<ctime> #include<queue> #include<stack> #include<vector> #include<cctype> #include<utility> #include<algorithm> #include<cstring> #include<string> #include<map> #include<set> #include<bitset> #include<deque> #include<cstdlib> #define INF 2147483646 #define ll long long #define db double #define min(x,y) (x>y?y:x) #define max(x,y) (x>y?x:y) using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } inline void put(int x) { x<0?putchar(‘-‘),x=-x:0; int num=0;char ch[70]; while(x)ch[++num]=x%10+‘0‘,x/=10; num==0?putchar(‘0‘):0; while(num)putchar(ch[num--]); putchar(‘\n‘);return; } const int MAXN=1003; int n,m,s1,s2,t; int ans,maxx; int a[MAXN][MAXN]; int b[MAXN],vis[MAXN][MAXN]; int f[MAXN][MAXN]; int g[MAXN][MAXN],w[MAXN][MAXN];//f[i][j]表示到了第i j个点所得到的价值最大 int main() { //freopen("1.in","r",stdin); freopen("tower.in","r",stdin); freopen("tower.out","w",stdout); memset(a,0,sizeof(a)); n=read();m=read(); for(int i=1;i<=n;++i) for(int j=1;j<=i;++j) a[i][j]=read(); for(int i=1;i<=n;++i) for(int j=1;j<=i;++j) { f[i][j]=max(f[i][j],f[i-1][j]+a[i][j]); f[i][j]=max(f[i][j],f[i-1][j-1]+a[i][j]); } for(int i=n;i>=1;--i)for(int j=1;j<=i;++j) { g[i][j]=max(g[i][j],g[i+1][j]+a[i][j]); g[i][j]=max(g[i][j],g[i+1][j+1]+a[i][j]); } //for(int i=1;i<=n;++i)maxx=max(maxx,f[n][i]); maxx=g[1][1]; for(int i=1;i<=n;++i) { for(int j=1;j<=i;++j)if(g[i][j]+f[i][j]-a[i][j]==maxx){vis[i][j]=1;break;} for(int j=1;j<=i;++j) { if(vis[i][j])continue; b[i]=max(g[i][j]+f[i][j]-a[i][j],b[i]); //cout<<b[i]<<endl; } } //puts(""); for(int i=1;i<=m;++i) { int x,y; x=read();y=read(); //cout<<vis[x][y]<<endl; if(x==1&&y==1){puts("-1");continue;} if(vis[x][y])put(b[x]); else put(maxx); } return 0; }

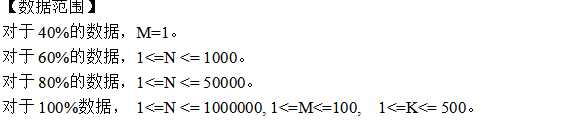
这道题 就很有意思了,是这几道题我暴力都写的比较难受的一道想出设多维来想办法进行状态转移 我觉得不管怎样转移都是具有极强的后效性的,2h后放弃了对于m==1的情况 我写了一个n^2k的暴力dp 写完了还觉得没什么问题 事实上我这种做法是不必要的。
考虑 m==1怎么写其实无非就是对于一个长度为n的序列 分成m+1段然后使每一段的价值等差数列的和的和最小。其实直接分就好了不需要dp
可能很显然的想出这是正确的,然后 无非是余数的问题 考虑每一段后都跟一个余数直至把余数数完。
那对于每一个窝的 我们使用k次以后这个窝所带来的价值 其实现在问题再次转换 转换成了 m个窝 k次清空操作 然后询问最小价值。
显然了 这是一个资源分配类型的dp 直接dp 转移一下就好了。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cmath> #include<cstdio> #include<ctime> #include<queue> #include<stack> #include<vector> #include<cctype> #include<utility> #include<algorithm> #include<cstring> #include<string> #include<map> #include<set> #include<bitset> #include<deque> #include<cstdlib> #define ll long long #define db double #define min(x,y) (x>y?y:x) #define INF 21474836460000000ll using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } inline void put(ll x) { x<0?putchar(‘-‘),x=-x:0; int num=0;char ch[70]; while(x)ch[++num]=x%10+‘0‘,x/=10; num==0?putchar(‘0‘):0; while(num)putchar(ch[num--]); putchar(‘\n‘);return; } const int MAXN=1000002,maxn=102,Maxn=502; ll n,m,p,T; ll ans; ll a[MAXN],c[maxn]; //对于 m==1 显然采用贪心可以 将一段序列分成p+1段的最小值 取平均即可 ll w[maxn][Maxn];//w[i][j]表示 对于第i种物品分成j段的代价 ll f[maxn][Maxn];//表示前i种牛分配到j个清理 得到了多少价值 ll cost(ll x,ll y) { ++y; ll cnt=x/y; ll mod=x%y; return ((cnt+1)*cnt/2)*y+mod*(cnt+1); } int main() { //freopen("1.in","r",stdin); freopen("noise.in","r",stdin); freopen("noise.out","w",stdout); n=read();m=read();p=read(); for(int i=1;i<=n;++i)a[i]=read(),++c[a[i]]; for(int i=1;i<=m;++i) for(int j=0;j<=p;++j)w[i][j]=cost(c[i],j); for(int i=1;i<=m;++i) for(int j=0;j<=p;++j) { f[i][j]=INF; for(int k=0;k<=j;++k) f[i][j]=min(f[i][j],f[i-1][k]+w[i][j-k]); } put(f[m][p]); return 0; }
其实很简单 但是针对m==1的情况我没有好好的思考所以 造成了整道题的崩溃。或者说我对模板只是感觉简单并没有利用它。
值得一提的是上述式子还可以进行单调性优化时间复杂度为mk 发现n>mk时间复杂度为O(n)(哇如此优秀。

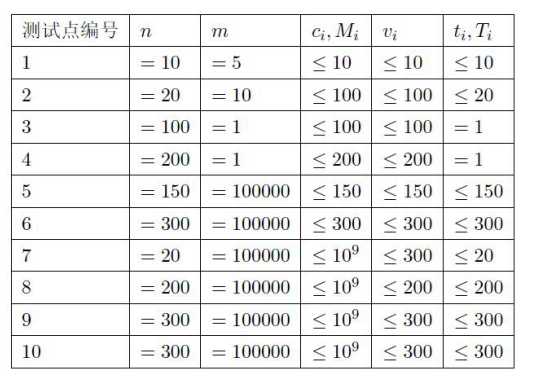
这道题的暴力超级好 直接01背包都有40分 加两个排序可以做到Mn的复杂度了。期望得分60 实际得分:60;
考虑后40分怎么办。看出M非常的大v非常的小 这又是01背包的变换形式了 仔细思考我们背包是根据容量来确定价值的,容量一定价值一定、
那如果是根据价值来确定容量呢 这样的01背包也是可以的吧 这样就价值为多少的时候 需要的金钱数。
显然 这个01背包的变形 是没有那么简单的,需要考虑 时间 这个我们按照时间排序物品即可。然后在f数组里进行二分查找即可。
细节需要处理 f数组可能不具单调性 O(n)扫一遍使其具有单调性即可。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cmath> #include<cstdio> #include<ctime> #include<queue> #include<stack> #include<vector> #include<cctype> #include<utility> #include<algorithm> #include<cstring> #include<string> #include<map> #include<set> #include<bitset> #include<deque> #include<cstdlib> #define ll long long #define db double #define min(x,y) (x>y?y:x) #define INF 21474836460000ll #define v(x) t[x].v #define w(x) t[x].w #define ti(x) t[x].ti using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } inline void put(int x) { x<0?putchar(‘-‘),x=-x:0; int num=0;char ch[70]; while(x)ch[++num]=x%10+‘0‘,x/=10; num==0?putchar(‘0‘):0; while(num)putchar(ch[num--]); putchar(‘\n‘);return; } const int MAXN=100002,maxn=302; int n,m,maxx,flag=1; struct wy { int w,v,ti; int friend operator <(wy x,wy y){return x.ti<y.ti;} }t[maxn]; struct wy1 { int x,y;//x为时间y为金钱 }s[MAXN]; ll f[maxn][maxn*maxn];//f[i][j]表示前i个物品 价值为j的最小花费 inline int find(int xx) { int l=0,r=n; while(l+1<r) { int mid=(l+r)>>1; if(ti(mid)<=xx)l=mid; else r=mid; } if(ti(r)<=xx)return r; return l; } inline int carculate(int i,int x) { int l=0,r=maxx; while(l+1<r) { int mid=(l+r)>>1; if(f[i][mid]<=x)l=mid; else r=mid; } if(f[i][r]<=x)return r; return l; } int main() { //freopen("1.in","r",stdin); freopen("market.in","r",stdin); freopen("market.out","w",stdout); n=read();m=read(); for(int i=1;i<=n;++i) { w(i)=read(); v(i)=read(); ti(i)=read(); maxx+=v(i); } //put(maxx); sort(t+1,t+1+n); for(int i=1;i<=m;++i)s[i].x=read(),s[i].y=read(); for(int i=1;i<=maxx;++i)f[0][i]=INF; f[0][0]=0; for(int i=1;i<=n;i++) for(int j=maxx;j>=0;j--) { f[i][j]=f[i-1][j]; if(j>=v(i))f[i][j]=min(f[i-1][j-v(i)]+w(i),f[i][j]); } for(int i=1;i<=n;++i) for(int j=maxx-1;j>=0;--j)f[i][j]=min(f[i][j+1],f[i][j]); for(int i=1;i<=m;++i) { int xx=find(s[i].x); //put(xx); put(carculate(xx,s[i].y)); } return 0; }
值得一提的是01二维01背包 注意不要少一句话承接上一层的值 我wa了半天因为这个。时间复杂度为 n*价值和+mlogn+mlog价值和+nlogn
一维的01背包 时间复杂度 n*价值和+nlogn+mlogm+mlogm+mlogm上下比较上面更为优秀 少了两次排序对了一次二分查找。
代码中的细节还算是比较ex的 调了一会才发现又犯sb错误。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cmath> #include<cstdio> #include<ctime> #include<queue> #include<stack> #include<vector> #include<cctype> #include<utility> #include<algorithm> #include<cstring> #include<string> #include<map> #include<set> #include<bitset> #include<deque> #include<cstdlib> #define ll long long #define db double #define min(x,y) (x>y?y:x) #define INF 21474836460000ll #define v(x) t[x].v #define w(x) t[x].w #define ti(x) t[x].ti using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } inline void put(int x) { x<0?putchar(‘-‘),x=-x:0; int num=0;char ch[70]; while(x)ch[++num]=x%10+‘0‘,x/=10; num==0?putchar(‘0‘):0; while(num)putchar(ch[num--]); putchar(‘\n‘);return; } const int MAXN=100002,maxn=302; int n,m,maxx,flag=1; struct wy { int w,v,ti; int friend operator <(wy x,wy y){return x.ti<y.ti;} }t[maxn]; struct wy1 { int x,y;//x为时间y为金钱 int id; int ans; }s[MAXN]; int cmp(wy1 a,wy1 b){return a.x<b.x;} int cmp1(wy1 a,wy1 b){return a.id<b.id;} ll f[maxn*maxn];//f[i][j]表示前i个物品 价值为j的最小花费 inline int carculate(int x) { int l=0,r=maxx; while(l+1<r) { int mid=(l+r)>>1; if(f[mid]<=x)l=mid; else r=mid; } if(f[r]<=x)return r; return l; } int main() { //freopen("1.in","r",stdin); freopen("market.in","r",stdin); freopen("market.out","w",stdout); n=read();m=read(); for(int i=1;i<=n;++i) { w(i)=read(); v(i)=read(); ti(i)=read(); maxx+=v(i); } //put(maxx); sort(t+1,t+1+n); for(int i=1;i<=m;++i)s[i].x=read(),s[i].y=read(),s[i].id=i; sort(s+1,s+1+m,cmp); for(int i=1;i<=maxx;++i)f[i]=INF; for(int i=1;i<=n;++i) { if(s[flag].x<ti(i)&&flag<=m) for(int j=maxx-1;j>=0;--j)f[j]=min(f[j],f[j+1]); while(s[flag].x<ti(i)&&flag<=m)s[flag].ans=carculate(s[flag].y),++flag; for(int j=maxx;j>=v(i);--j)f[j]=min(f[j],f[j-v(i)]+w(i)); } if(flag<=m)for(int j=maxx-1;j>=0;--j)f[j]=min(f[j],f[j+1]); for(int i=flag;i<=m;++i)s[i].ans=carculate(s[i].y); sort(s+1,s+1+m,cmp1); for(int i=1;i<=m;++i)put(s[i].ans); return 0; }

这道题 我感觉是上面的题目中最难的题目原因是 感觉无论怎么选后效性极强。于是对着40分写了一个爆搜。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cmath> #include<cstdio> #include<ctime> #include<queue> #include<stack> #include<vector> #include<cctype> #include<utility> #include<algorithm> #include<cstring> #include<string> #include<map> #include<set> #include<bitset> #include<deque> #include<cstdlib> #define ll long long #define db double #define min(x,y) (x>y?y:x) #define INF 2147483646 #define v(x) t[x].v #define w(x) t[x].w #define ti(x) t[x].ti using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } inline void put(int x) { x<0?putchar(‘-‘),x=-x:0; int num=0;char ch[70]; while(x)ch[++num]=x%10+‘0‘,x/=10; num==0?putchar(‘0‘):0; while(num)putchar(ch[num--]); putchar(‘\n‘);return; } const int MAXN=20; int n,ans; int vis[MAXN],v[MAXN],w[MAXN]; int q[MAXN],t; void dfs(int depth) { if(depth<=n&&depth) { int cnt=0,sum=0; for(int i=1;i<=depth;++i) { sum+=v[q[i]]-cnt; cnt+=w[q[i]]; } ans=max(ans,sum); if(depth==n)return; } for(int i=1;i<=n;++i) { if(vis[i]==0) { q[depth+1]=i; vis[i]=1; dfs(depth+1); vis[i]=0; } } } int main() { //freopen("1.in","r",stdin); freopen("value.in","r",stdin); freopen("value.out","w",stdout); n=read(); if(n<=10) { for(int i=1;i<=n;++i)v[i]=read(),w[i]=read(); dfs(0); } put(ans); return 0; }
显然爆搜不是搜全排列连子排列都要搜出来。然后计算答案即可。复杂度 8!其实子排列可以创造出全排列所以 复杂度认为8!
那好我要开车了,针对这道题老师也是点了一下思路接下来是我今天的分析这道题怎么写。
1 首先我们要选的话一定选wi较小的,因为我们如果还想选下一个的话 首先对于这两个物品 其最小的wi必然是被先选的 然后剩下的那个价值量会减小很少的 如果选wi较大的那么价值就会减小很大。反而不优了。需要按wi排一下序。
2 首先我们f[i][j]表示前i件物品选择j件物品的最大价值那么此时价值会灰常不好算因为我们不知道后面还要选多少个物品。
3 那么显然 f[i][j]表示前i件物品中选择后j个物品的最大价值。这样来进行就可以了。
注意排序是必然的因为 wi较小的选择是必然的 而且观察我们这个状态 选择了后j个物品 显然这个选择了后j个物品我们进行状态转移时如果不倒序就无法进行有效的状态转移,因为你的状态为空。当然记忆化搜索也行 反正都是拓扑序。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cmath> #include<cstdio> #include<ctime> #include<queue> #include<stack> #include<vector> #include<cctype> #include<utility> #include<algorithm> #include<cstring> #include<string> #include<map> #include<set> #include<bitset> #include<deque> #include<cstdlib> #define ll long long #define db double #define min(x,y) (x>y?y:x) #define INF 2147483646 #define v(x) t[x].v #define w(x) t[x].w #define ti(x) t[x].ti using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } inline void put(int x) { x<0?putchar(‘-‘),x=-x:0; int num=0;char ch[70]; while(x)ch[++num]=x%10+‘0‘,x/=10; num==0?putchar(‘0‘):0; while(num)putchar(ch[num--]); putchar(‘\n‘);return; } const int MAXN=5002; int n,maxx; int f[MAXN][MAXN];//f[i][j] 表示 对于前i个物品 后面选择j个物品的最大价值 struct wy { int v,w; int friend operator <(wy x,wy y) { return x.w>y.w; } }t[MAXN]; int main() { freopen("1.in","r",stdin); //freopen("value.in","r",stdin); //freopen("value.out","w",stdout); n=read(); for(int i=1;i<=n;++i)v(i)=read(),w(i)=read(); sort(t+1,t+1+n); //for(int i=1;i<=n;++i)cout<<w(i)<<endl; for(int i=1;i<=n;++i) { for(int j=1;j<=i;++j) { f[i][j]=max(f[i-1][j],f[i-1][j-1]+v(i)-w(i)*(j-1)); maxx=max(maxx,f[i][j]); } } put(maxx); return 0; }


对于这道题 其实最暴力也最简单的是最短路问题 由于是树也就最短路只有一条直接dfs即可 然后也变成了一个树形换根dp
所幸这道题比较简单我仔细思考之后是独立的写出来了 这种换根还是比较简单的。
考虑到我们已经求出的东西能给我们带来什么效果。
设出f[i][0]表示以其为根的子树内到此点的距离之和 d[i]表示以i为根的子树的人数 f[i][1]表示以i为中心的最小不方便值。
对于我们第一次dfs 求出 f[i][0] & d[i] 此时我以1为根 那么显然 f[1][0]=f[1][1];
然后通过f[1][1] 进行换根dp 状态转移很好推 f[tn][1]=f[tn][0]+f[x][1]-f[tn][0]-d[tn]*e[i]+(cnt-d[tn])*e[i];

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cmath> #include<cstdio> #include<ctime> #include<queue> #include<stack> #include<vector> #include<cctype> #include<utility> #include<algorithm> #include<cstring> #include<string> #include<map> #include<set> #include<bitset> #include<deque> #include<cstdlib> #define ll long long #define db double using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline ll read() { ll x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } inline void put(ll x) { x<0?putchar(‘-‘),x=-x:0; ll num=0;char ch[70]; while(x)ch[++num]=x%10+‘0‘,x/=10; num==0?putchar(‘0‘):0; while(num)putchar(ch[num--]); putchar(‘\n‘);return; } const ll MAXN=200002; ll n,len; ll cnt,ans=100000000000000000ll; ll f[MAXN][2];//f[i][0]表示以i为根节点且不为集会地点时的方便程度 ll d[MAXN],a[MAXN];//d[i]表示以1为根节点时的牛数 ll lin[MAXN<<1],nex[MAXN<<1],ver[MAXN<<1]; ll e[MAXN<<1]; inline ll min(ll x,ll y){return x>y?y:x;} inline void add(ll x,ll y,ll z) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; e[len]=z; } inline void dp(ll x,ll father) { d[x]=a[x]; for(ll i=lin[x];i;i=nex[i]) { ll tn=ver[i]; if(tn==father)continue; dp(tn,x); f[x][0]+=d[tn]*e[i]+f[tn][0]; d[x]+=d[tn]; } return; } void dfs(ll x,ll father) { for(ll i=lin[x];i;i=nex[i]) { ll tn=ver[i]; if(tn==father)continue; f[tn][1]=f[tn][0]+(cnt-d[tn])*e[i]+f[x][1]-d[tn]*e[i]-f[tn][0]; dfs(tn,x); } return; } int main() { //freopen("1.in","r",stdin); freopen("gather.in","r",stdin); freopen("gather.out","w",stdout); n=read(); for(ll i=1;i<=n;++i)a[i]=read(),cnt+=a[i]; for(ll i=1;i<n;++i) { ll x,y,z; x=read();y=read();z=read(); add(x,y,z);add(y,x,z); } dp(1,0); f[1][1]=f[1][0]; dfs(1,0); for(ll i=1;i<=n;++i)ans=min(ans,f[i][1]); //for(ll i=1;i<=n;++i)put(f[i][1]); put(ans); return 0; }

这是压轴的dp 了我感觉一般吧 还算是比较基础的决策优化 但是这个优化和平常的不太一样 ,我感觉是比较难受的优化。
对于40分考虑一个 n^2的做法 设 f[MAXN];//f[i]表示前i个原子分成若干段的最小代价
显然状态转移f[i]=min(f[i],f[j]+cost[j+1][i]); 当且仅当 j+1~i 不起任何冲突。这个不起冲突我是一个区间dp 来写的麻烦了O(n)即可。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cmath> #include<cstdio> #include<ctime> #include<queue> #include<stack> #include<vector> #include<cctype> #include<utility> #include<algorithm> #include<cstring> #include<string> #include<map> #include<set> #include<bitset> #include<deque> #include<cstdlib> #define ll long long #define db double #define min(x,y) (x>y?y:x) #define INF 2147483646 #define v(x) t[x].v #define w(x) t[x].w #define ti(x) t[x].ti using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } inline void put(int x) { x<0?putchar(‘-‘),x=-x:0; int num=0;char ch[70]; while(x)ch[++num]=x%10+‘0‘,x/=10; num==0?putchar(‘0‘):0; while(num)putchar(ch[num--]); putchar(‘\n‘);return; } const int MAXN=1002; int n; int a[MAXN],b[MAXN]; int w[MAXN][MAXN],cost[MAXN][MAXN]; int f[MAXN];//f[i]表示前i个原子分成若干段的最小代价 int main() { //freopen("1.in","r",stdin); freopen("array.in","r",stdin); freopen("array.out","w",stdout); n=read(); memset(f,0x3f3f3f3f,sizeof(f)); for(int i=1;i<=n;++i) { a[i]=read();b[i]=read(); w[i][i]=0;cost[i][i]=b[i]; } for(int len=2;len<=n;++len) { for(int i=1;i<=n-len+1;++i) { int j=i+len-1; w[i][j]|=w[i][j-1]; w[i][j]|=w[i+1][j]; w[i][j]|=(a[i]==a[j]?1:0); cost[i][j]=max(cost[i][j-1],b[j]); } } /*for(int i=1;i<=n;++i) for(int j=i;j<=n;++j) cout<<i<<‘ ‘<<j<<‘ ‘<<w[i][j]<<endl;*/ f[0]=0; for(int i=1;i<=n;++i) for(int j=0;j<i;++j) { if(!w[j+1][i])f[i]=min(f[i],f[j]+cost[j+1][i]); } put(f[n]); return 0; }
考虑100分的做法 刚刚那个不起冲突可以O(n) 但是总dp式其实就是一个n^2的 优化其实是 观察决策具有单调性。
真的是有单调性啊 尽管不太明显 但是 我仍是为出题人感动 这都有单调性真是为了防AK的题目没有2个小时拿不下来。。(对我来说是这样的
大雾! 单调性在 很隐秘的地方 首先 对于 f数组 f[j]<=f[i] j<=i f数组单调不下降 对于cost数组呢貌似状似形似 也是一个单调的 是一个单调不上升的 因为如果有一个更大的cost 那么这整个区间都将被更新成这个cost值。一个单调不下降一个单调不上升很烦。这里我们把f[j]可以抽象成一个点 而cost 抽象成一个区间 显然对于cost形成的每一个区间我们选择那个区间最左边的决策时最优秀的。我这样说就把问题规划的很清楚了 我好棒!
其实对于每一个i 最左边的端点 确定然后就是i-最左边端点之中寻找一个 决策使其最优当然对于cost划分的不同的区域我们尽量选择靠近左边的端点这样有了单调性 考虑用什么来维护这个东西 单调队列?貌似不行因为这样的话不只是队首造成贡献了 这个队伍很可能整个都会造成贡献 线段树?
貌似不太行 因为f[j]不会变 cost 会变随着i的增加 这个区域的本质会改变我们修改cost的区间 经过和同学的一番讨论 我 更加深刻的理解了这道题的优化过程 首先是 单调队列 q 维护cost 单调不下降的的区间的左端点 其实就是在众多的不合法区间之内寻找到一个最优的决策。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cmath> #include<cstdio> #include<ctime> #include<queue> #include<stack> #include<vector> #include<cctype> #include<utility> #include<algorithm> #include<cstring> #include<string> #include<map> #include<set> #include<bitset> #include<deque> #include<cstdlib> #define ll long long #define db double #define min(x,y) (x>y?y:x) #define INF 2147483646 #define v(x) t[x].v #define w(x) t[x].w #define ti(x) t[x].ti using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } inline void put(int x) { x<0?putchar(‘-‘),x=-x:0; int num=0;char ch[70]; while(x)ch[++num]=x%10+‘0‘,x/=10; num==0?putchar(‘0‘):0; while(num)putchar(ch[num--]); putchar(‘\n‘);return; } const int MAXN=100002; int n,flag; int a[MAXN],b[MAXN],last[MAXN]; int q[MAXN],l,r; int f[MAXN]; int main() { //freopen("1.in","r",stdin); freopen("array.in","r",stdin); freopen("array.out","w",stdout); n=read(); for(int i=1;i<=n;++i)a[i]=read(),b[i]=read(),f[i]=INF; q[++r]=0;++l; for(int i=1;i<=n;++i) { if(last[a[i]])flag=max(flag,last[a[i]]); last[a[i]]=i; while(l<=r&&q[l]<=flag)++l; while(l<=r&&b[q[r]]<=b[i])--r; q[++r]=i; for(int j=l+1;j<=r;++j)f[i]=min(f[i],f[q[j-1]]+b[q[j]]); f[i]=min(f[i],f[flag]+b[q[l]]); } put(f[n]); return 0; }
这个直接在单调队列中寻找决策了 貌似是可以直接加进set里 logn寻找最优决策。
利用find的话直观性很差 但是 可以照着上面的板子打就不容易出现错误了 这里我采用的是迭代器的做法。
其实就很显然了加上一个set 即可 。线段树的我觉得不太行写不了。

//#include<bits/stdc++.h> #include<iostream> #include<iomanip> #include<cmath> #include<cstdio> #include<ctime> #include<queue> #include<stack> #include<vector> #include<cctype> #include<utility> #include<algorithm> #include<cstring> #include<string> #include<map> #include<set> #include<bitset> #include<deque> #include<cstdlib> #define ll long long #define db double #define min(x,y) (x>y?y:x) #define INF 2147483646 #define v(x) t[x].v #define w(x) t[x].w #define ti(x) t[x].ti using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } inline void put(int x) { x<0?putchar(‘-‘),x=-x:0; int num=0;char ch[70]; while(x)ch[++num]=x%10+‘0‘,x/=10; num==0?putchar(‘0‘):0; while(num)putchar(ch[num--]); putchar(‘\n‘);return; } const int MAXN=100002; int n,flag; int a[MAXN],b[MAXN],last[MAXN]; int q[MAXN],l,r; int f[MAXN]; set<pair<int,int> > s; set<pair<int,int> > :: iterator id[MAXN]; int main() { freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;++i)a[i]=read(),b[i]=read(),f[i]=INF; q[++r]=0;++l;s.insert(make_pair(0,0)); id[q[r]]=s.find(make_pair(0,0)); for(int i=1;i<=n;++i) { if(last[a[i]])flag=max(flag,last[a[i]]); last[a[i]]=i; while(l<=r&&q[l]<=flag) { s.erase(id[q[l]]); ++l; } while(l<=r&&b[q[r]]<=b[i]) { s.erase(id[q[r]]); --r; } q[++r]=i; if(s.begin()!=s.end())f[i]=(*s.begin()).first; f[i]=min(f[i],f[flag]+b[q[l]]); s.insert(make_pair(f[i],b[i+1])); id[q[r]]=s.find(make_pair(f[i],b[i+1])); } put(f[n]); return 0; }
那么这几dp 题目总结到这里 关键是观察决策。
老师说 要对模型有深刻的理解 有的时候往往想不出来的问题都是没有把问题转换好 所以才 不会做。
这几道题都是对模型的升华 也算是比较有意义和价值的。
原文:https://www.cnblogs.com/chdy/p/10804597.html

