The Complete Diffie-Hellman Key Exchange Diagram

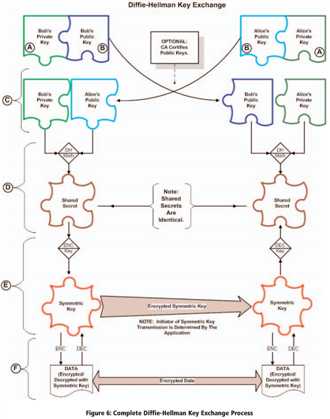
• The process begins when each side of the communication generates a private key. Each side then generates a public key (letter B), which is a derivative of the private key.
• The two systems then exchange their public keys. Each side of the communication now has its own private key and the other system‘s public key (see the area labeled letter C in the diagrams).
• Once the key exchange is complete, the process continues. The DH protocol generates "shared secrets"—identical cryptographic keys shared by each side of the communication.
• The shared secret encrypts a symmetric key for one of the symmetric algorithms, transmits it securely, and the distant end decrypts it with the shared secret.

The Amateur Mathematician‘s Explanation for "DH Math"

?

Using a common number, both sides use a different random number as a power to raise the common number. The results are then sent to each other. The receiving party raises the received number to the same random power they used before, and the results are the same on both sides. It‘s very clever. There is more computation in actual practice, but this example, which uses tiny numbers to illustrate the concept, shows a very clever mathematical approach. Each party raises the common number which is 2 in this example (this has nothing to do with binary—it is just the number "2") to a random power and sends the result to the other. The received number is raised to the same random power. Note that both parties come up with the same secret key, which was never transmitted intact.

?

?

SRC=https://learningnetwork.cisco.com/.../WP_Palmgren_DH.pdf

Diffie-Hellman Key Exchange – A Non-Mathematician’s Explanation,布布扣,bubuko.com

原文：http://www.cnblogs.com/coryxie/p/3857434.html