[微信机器人_04]自然语言处理简单实现

对于两个正整数，由欧拉定理可知，存在正整数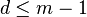， 比如说欧拉函数，即小于等于 m 的正整数中与 m 互质的正整数的个数，使得。

由此，在时，定义对模的指数为使成立的最小的正整数。由前知 一定小于等于 ，若，则称是模的原根。

摘自维基百科

这个题目就是要求一个质数n的最大的原根

现在的问题就是怎么求原根，如果直接暴力是 O(nlogn * 因子数)，显然是不行的。。

方法：

如果q不是n的原根，那么必然存在一个t < n-1且 q^t = 1(mod n)，这里我就假设q^t = 1(mod n)， t肯定是整除n-1的(想想就明白)

根据裴蜀定理可知ax+by=gcd(a,b)必然有解

所以必然存在tx + (n-1)y = gcd(t, n-1)，所以q^(tx) = 1 = q^( -(n-1)y + gcd(t, n-1)) = q^( gcd(t, n-1) ) ，即q^( gcd(t, n-1) ) = 1

因为t < n-1 且t 整除n-1，所以 t 至少整除 (n-1)/pi (1 <= i <=  tot)中的一个，pi为n-1的素因子

所以要判断q是不是n的原根，只需要判断 q^( (n-1)/pi ) % n 其中如果有一个等于1的话，那q就不是原根！

代码：

原文：http://blog.csdn.net/elcarim/article/details/18527575